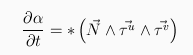
This short review is about surface matching. Surface matching (and more generally the matching of structures) is an important subject of computer vision, which has given rise to an important amount of research papers. This presentation is made of two sections: we will first give a broad overview of the terminology used in the problem of matching, together with a few standard references, and we will focus on a new method for surface matching developped by the authors.
The problem of matching structures is a challenging issue in computer
vision and graphics. It has a large number of applications. The
definition of structures characteristics depends on the problem
addressed. We can however characterize the matching algorithm
based on the structures of interest: points, lines, curves, surfaces
and volumes, depending on the application. One can cite: point
matching techniques (with use of correlation based and signal
matching techniques) , the matching of 2D points with 2D structures,
2D points with 3D structures, 3D points with 3D structures, clustering
and accumulation array techniques, relaxation based techniques
, principal component decompositions, point features), the matching
of linear structures ( 2D lines with 2D structures etc.), matching
areas, regions, surfaces (piecewise segment matching of contours,
image to 3D surface matching), the problems of matching occuring
in image and sensor fusion. For all these topics, we recommend
the following web site [1], which contains an extensive bibliography in computer vision,
and, notably on matching and registration (section 12).
A general matching formulation problem can be stated as: given
two structures S and D define a function which associates to any
point of S a corresponding point on D. The characterization of
such function is an ill-posed problem in the sense there is no
unique solution. However, introducing structures properties such
as their geometry or the underlying image representation allows
to characterize a unique matching function. For instance in [14] one seeks a rotation and translation that maps a first object
onto a second. The problem of matching surfaces is also very important
in surface registration ([2,3,8,9,13]), range view registration ([6,7,12]). Specific data levels of representation can be defined to ease
the process of surface matching [4,5,11]. This idea is developped by A. E. Johnson in his PhD thesis where
the concept of spin image is introduced ([10]). Commonly used features are pixel grey level values for stereoscopic
matching or optical flow [15], edges for token based approaches [16] and geometric properties of the structures [17,18]. The latter properties are more robust since they can deal with
situations where there is no consistency of image grey level.
Relevant geometrical properties are selected on the basis of their
ability to characterize a description of the structures which
is invariant to the considered deformation. In the case of rigid
or small elastic deformations high curvature points [19,20] or semi-differential invariants [21] can be considered as an invariant description of the structure.
Higher order geometric description can also be considered such
as crest and ridge lines in order to characterize volume structures
properties [22]. Such methods perform well in the case of small deformation but
cannot deal large deformation and topological change. Such problems
occurs when we are interested in studying the evolution of a structure
whose topology evolves in time [23]. This situation is very common in computer graphics where we
are interested in defining a morphing function, i.e. a set of
paths departing from the source S and ending at the destination
structure D. Here the matching criterion translates into geometric
constraints on the paths themselves [24]. Matching features in 3D images is also an important task in
3D medical image analysis. In this later field, specific matching
techniques have been developped for brain mapping and the matching
of cortical patterns. Thompson and Toga, 1996 (see the web page
[25]) generate a correspondance in 3D from a vector field. A method
for the computation of a matching function from the diffeomorphisms
generated by a vector field is also presented in [26]. See also G. Christensen's work [27].
In [33,35] a new method for surface matching with large deformation and
arbitrary topological changes is presented. It relies on a surface
evolution scheme generalizing a curve evolution process [29] and makes use of a level-set formulation [28,30,31,32]. It generalizes the curve matching process presented in [34] and is briefly described in the next section.
Source code and executables: See the Mesh Toolbox software libraries and executables: http://www.cs.cmu.edu/~3dvision/meshtoolbox/executables.html.
The surface matching technique presented in this section has the following advantages:
The matching method proposed by the authors consists first in generalizing the curve evolution process presented in [29]. Such a generalization leads to the computation of distance maps for surfaces embedded in 3-manifolds, and provides an efficient computational tool for realizing a surface matching in a very general case. Let W be a 3-manifold in 4D, let X0 be an initial surface drawn on W. We seek an evolution equation governing the propagation of surfaces Xt in W located at geodesic distance t from X0. The equation evolution may be found by considering an orthogonal parametrization for Xt, and has the form:
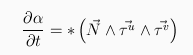
In this equation, N is the normal to W, alpha(u,v) is a local orthogonal parametrization of Xt (parameters u and v), tauu and tauv are the unitary tangent vectors to Xt. The * symbol refers to the Hodge operator, which provides an efficient and easy computational tool for cross-products in dimensions 4 or even n. To derive an equation related to the computation of distances maps, one considers the orthogonal projection of surfaces Xt onto the xyz hyperplan in 4D space. Writing that projection in the form of a level-set with potential function phi, the following equation is derived:
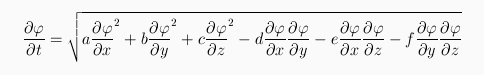
where the quantities a,b,c,d,e and f are differential attributes of the manifold W and can be pre-computed once and for all prior to running the evolution process. The numerical resolution is derived by using an explicit scheme with a multi-grid method. It is robust and stable, although it may also be computationally intensive. By using a potential function coming from a distance map for the initial surface X0, one sees that the previous equation generates the values of a distance map on a "cost manifold" W. It is worthwile to notice that the previous equations can be wrtiiten in a more compact form:
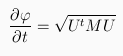
M being the matrix of a quadratic form, generalizing the 2D case presented in [29]. This remark yields to a generalization in n-dimensional space, where the matrix M becomes:

(the pij are differential attributes of the manifold W) and U is the vector
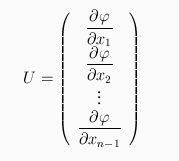
Now let us suppose that one wants to match two surfaces S and D. This is accomplished by the following steps:
In the next section,we give some examples, both synthetic and with real images.
1. Matching between two spheres and an ellipsoid.

Result of the matching between 2 yellow spheres and a red ellipsoid. The matching paths are drawn. This example illustrates, on a synthetic example, large deformation and change of topology.
2. Matching between two spheres and an ellipsoid. (mpeg animation)
3. Example computed with real-world images.
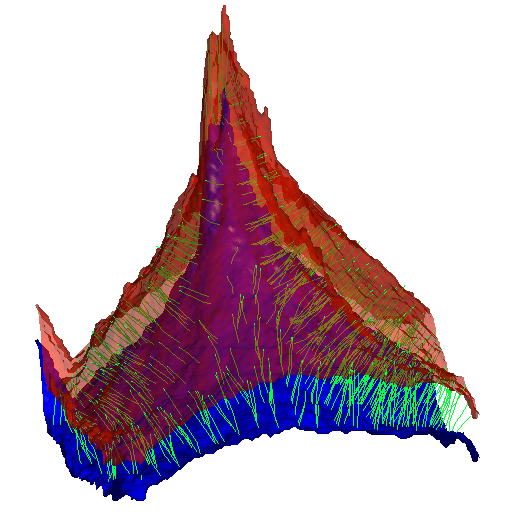
Result of the matching between a surface built from a DEM (digital elevation model) of Mount Etna, and the same image after the application of a geophysical model of a volcanic eruption ( Mogi model).