
This teach file is an introduction to convolution, an important operation in low-level vision.
Please read the introduction giving general information about the nature of this document.
You should have read through TEACH VISION1 and run the examples.
Load the libraries needed to run the examples now:
uses popvision ;;; search vision libraries
uses rci_show ;;; image display utility
uses showarray ;;; array printing utility
uses arrayfile ;;; array storage utility
uses arraysample ;;; sampling utility
uses float_byte ;;; type conversion utility
uses float_arrayprocs ;;; array arithmetic library
uses convolve_2d ;;; convolution program
We will also use the same image as before, so we might as well read it now. It will speed up the examples if we convert the image array to a packed floating point representation; this makes little difference to how it is used in Pop-11, so you need not worry about this (but see HELP *FLOAT_BYTE if you want more details).
vars image; ;;; declare a permanent variable
arrayfile(popvision_data dir_>< 'stereo1.pic') -> image;
;;; convert from string array to packed float array
float_byte(image, false, false, 0, 255) -> image;
The example at the end of TEACH VISION1 processed an image to highlight vertical boundaries, by taking differences between the values of horizontally adjacent pixels. Each pixel had the value of the pixel to its left subtracted from it. Another way of describing this process begins by making a table or mask containing the values -1 and +1, like this:
-----------
| -1 | +1 |
-----------
We can now do our calculation by overlaying this mask on the array, multiplying each grey-level by the superimposed mask value, and adding the products. This must be done for each mask position in turn. For example, suppose we have an array with just 3 columns and 2 rows, containing these grey-level values:
----------------
| 22 | 25 | 53 |
|----+----+----|
| 17 | 20 | 66 |
----------------
Then the calculation for the top right hand element of the output array looks like:
----------------------------------
| |----------+----------|
| 22 || 25 x -1 | 53 x +1 |+---------
| |----------+----------| |
|----------+----------+----------| |
| | | | |
| 17 | 20 | 66 | |
| | | | | 25 x -1 + 53 x +1
---------------------------------- |
| = 28
----------- |
| 3 | 28 <--------------------
|----+----|
| 3 | 46 |
-----------
We repeat this calculation for all the other possible positions of the mask (including positions that overlap with each other) to fill in the other squares.
Although the multiplications may seen superfluous if all we want to do is to take differences, the advantage of this way of looking at the process is that it is easy to generalise. For example, we can specify a vertical differencing operation with the mask
------
| -1 |
|----|
| +1 |
------
and masks for nearest-neighbour diagonal differences look like
----------- -----------
| -1 | 0 | | 0 | -1 |
|----+----| |----+----|
| 0 | +1 | | +1 | 0 |
----------- -----------
The table of numbers that specifies a convolution is known as a mask, a kernel, an operator or a template, depending on the author, and the numbers in the mask are often called weights.
The natural way to represent a convolution mask in a program is to use an array, just as for an image. However, there is a small added complication: if we lay out the mask as above, then the rows and columns are numbered in the opposite directions to the rows and columns of the image array. Accepting that there is a very good reason for this, which we shall come to later, we can label the rows and columns of the horizontal differencing mask thus:
1 0
-----------
0 | -1 | +1 |
-----------
with the column numbers increasing from right to left.
The location of (0, 0) (i.e. column 0, row 0) in the mask is important: during convolution, each result will be placed in the output array at the location corresponding to the pixel lying under the (0, 0) mask element in the input array. Thus in the example above, if the value 53 lies at (3, 1) in the input array, the value 28 will lie at (3, 1) in the output array, because the value 28 is generated when the value 53 lies under the (0, 0) mask element. The labelling of rows and columns for the input and output arrays will therefore be as follows:
1 2 3 2 3
---------------- -----------
1 | 22 | 25 | 53 | 1 | 3 | 28 |
|----+----+----| -> |----+----|
2 | 17 | 20 | 66 | 2 | 3 | 46 |
---------------- -----------
Now we are in a position to set up a Pop-11 array to act as a convolution mask for horizontal differencing. Referring to the diagram of the mask above, the columns run from 0 to 1 and the rows from 0 to 0, so the boundslist of the array will be [0 1 0 0], and we can set up the mask as follows:
vars mask;
newarray([0 1 0 0]) -> mask; ;;; create a new array
-1 -> mask(1, 0); ;;; col 1, row 0
1 -> mask(0, 0); ;;; col 0, row 0
To try this out, we will use a library procedure for two-dimensional convolutions, and apply it to our test image.
vars newimage;
convolve_2d(image, mask, false, false) -> newimage;
As usual, you can refer to HELP *CONVOLVE_2D if you want more information about the procedure we have just used, but it is not necessary to do so now. The result, of course, should look identical to the last example of TEACH VISION1: to check, first print the output array to see the boundslist (note it starts at column 81 as it ought) and then display it:
newimage =>
prints:
** <array [81 176 64 191]>
rci_show(newimage) -> ;

You should now try out the vertical difference mask and the diagonal difference masks in the same way. Do not forget that row numbers in convolution masks increase upwards; if you have difficulty with the boundslists or setting the values in the arrays, try drawing out small diagrams like the ones above. (Continue just to give <false> as the last two arguments to convolve_2d.)
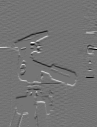


You should be able to see clearly how edges of different orientations stand out in the four different results. Remember that you can increase the size of the display windows by changing rci_show_scale if you wish.
It is possible to design a convolution mask that is sensitive to all edges, regardless of orientation. One of the simplest such masks is the small centre-surround mask that looks like this:
----------------------
| -1/8 | -1/8 | -1/8 |
|------+------+------|
| -1/8 | +1 | -1/8 |
|------+------+------|
| -1/8 | -1/8 | -1/8 |
----------------------
This mask is approximately isotropic - you can rotate it about its centre and it looks roughly the same - so that it will respond more or less equally to edges in any direction. If the operator is on a uniform patch of the image, its output is zero because the 8 weights of -1/8 will cancel out with the single +1. If it is close to an edge, so that there is an imbalance, then it will give a positive or negative output, depending on which side of the edge it is.
We can set up this mask and try it with the following code. Note that the central +1 is put at the (0, 0) position in the mask, which is the natural choice. This means that the value stored at (X, Y) in the output array is the value at (X, Y) in the input array, minus the average of its neighbours. We use the initialisation argument to newarray to set the whole mask to -1/8, then update the central value to +1.
newarray([-1 1 -1 1], -0.125) -> mask;
1 -> mask(0, 0);
convolve_2d(image, mask, false, false) -> newimage;
rci_show(newimage) -> ;

We will see how to make more effective use of the centre-surround mask later. Although centre-surround operations are important in theories of biological vision, practical computer vision systems tend to use masks which are more closely related to the vertical and horizontal difference operations.
This centre-surround mask implements an approximation to the mathematical operator known as the Laplacian; this in turn is closely related to taking the second derivative of a function. If you are familiar with these mathematical operations, you may be able to see the link. If you have not met the Laplacian before, but encounter it in a book or paper, it may help to understand it if you think in terms of the convolution mask shown above.
We often want to reduce the amount of small-scale detail in an image, either to get rid of irrelevant texture in trying to pick out the main shapes, or to reduce the effects of noise (random variations in the grey-level values) introduced by the camera optics or digitisation process. One way of doing this is to replace each grey-level by a local average of itself and its neighbours. Such averages tend to be done with 3 x 3 or 5 x 5 masks so that they can be symmetrical about their centres. For example, a 3 x 3 mask that implements a straight average, giving all 9 values the same weight, looks like
-------------------
| 1/9 | 1/9 | 1/9 |
|-----+-----+-----|
| 1/9 | 1/9 | 1/9 |
|-----+-----+-----|
| 1/9 | 1/9 | 1/9 |
-------------------
and is easily tried with
newarray([-1 1 -1 1], 1.0/9.0) -> mask;
convolve_2d(image, mask, false, false) -> newimage;
rci_show(newimage) -> ;

You will see that the result looks like a blurred version of the original image (which you should display if you have not already done so). This kind of mask is sometimes called a blurring mask as well as a smoothing mask.
To blur the image more heavily, you could use a larger mask, or alternatively, you could repeat the convolution one or more times:
convolve_2d(newimage, mask, false, false) -> newimage;
rci_show(newimage) -> ;

Note the picture getting increasingly fuzzy each time you execute the two lines of code above.
It is possible to combine more than one operation in a single mask. A good example is given by the Sobel masks for edge detection, which combine the vertical and horizontal differencing operations with some smoothing to reduce the effects of noise or very local texture.
The masks look like:
---------------- ----------------
| -1 | 0 | 1 | | -1 | -2 | -1 |
|----+----+----| |----+----+----|
| -2 | 0 | 2 | | 0 | 0 | 0 |
|----+----+----| |----+----+----|
| -1 | 0 | 1 | | 1 | 2 | 1 |
---------------- ----------------
The single values used in the simple differencers above are replaced by averages over 3 pixels, weighted towards the centre in each case. In addition, the positive and negative parts are separated by a one-pixel gap; by increasing the baseline for differencing this too has a smoothing effect, and it allows the mask to be more symmetrical, so that the results are "centred" in a way that is not true for the smaller difference operators.
You should now easily be able to set up the Sobel masks and look at their effects. Compare the outputs from the Sobel masks with the results of smoothing the image and then taking vertical or horizontal differences - the results should be similar, though not identical.
Why should the rows and columns of masks be numbered in the opposite directions to those of images? The reason is that with this convention, the operation of convolution is associative - that is, if two masks are convolved one with the other, then the result can be used as a mask that has the same effect as convolving each of the two masks with the image, one after the other. (If you decide to check this statement experimentally, note that you will have to extend one of the initial mask arrays with a border of zeroes to avoid losing any values in the compound mask.) Also, convolution is commutative - that is, you can exchange the mask and the image as far as the mathematics goes (extending the mask with a border of zeroes), though in practice this would result in absurdly inefficient programs.
You could skip the rest of this section on a first reading.
There is another way of looking at convolution which makes sense of the mask indices. It can be useful to have this other way of thinking about convolution.
This approach involves shifting copies of the array, multiplying the copies and the original by the weights, and adding them together. Taking horizontal differencing as an example again, we proceed as follows:
1. Make a copy of the image array, but with every value shifted, or offset, one pixel to the right - call this shift_image:
image shift_image
1 2 3 1 2 3 4
---------------- ---------------------
1 | 22 | 25 | 53 | 1 | - | 22 | 25 | 53 |
|----+----+----| |----+----+----+----|
2 | 17 | 20 | 66 | 2 | - | 17 | 20 | 66 |
---------------- ---------------------
2. Trim the edges of the arrays to retain only the values that are defined in both arrays (i.e. in this case remove columns 1 and 4).
3. Multiply every grey-level in the unshifted array by 1 and every grey-level in the shifted array by -1:
image x 1 shift_image x -1
2 3 2 3
----------- -------------
1 | 25 | 53 | 1 | -22 | -25 |
|----+----| |-----+-----|
2 | 20 | 66 | 2 | -17 | -20 |
----------- -------------
4. Add these two arrays, pixel by pixel, giving as the result:
2 3 2 3
----------------- -----------
1 | 25-22 | 53-25 | 1 | 3 | 28 |
|-------+-------| = |----+----|
2 | 20-17 | 66-20 | 2 | 3 | 46 |
----------------- -----------
Of course, this seems very cumbersome compared to the original procedure, and in fact the method just described would not be used in a practical program, unless one happened to have parallel hardware that was suited to it. It should be clear, however, that the results are identical.
In step 3 we multiplied the two arrays by 1 and -1. We can put these two values in a table, where position in the table corresponds to the offset of the array that was multiplied, thus:
0 1
-----------
0 | +1 | -1 |
-----------
The value at column 0, row 0 in this table specifies the multiplier for the unshifted array. The value at column 1, row 0 specifies the multiplier for the array shifted one column to the right.
This is, of course, just the same convolution mask as we had before, although it has now been drawn the other way round. However, the correct assignment of row and column indices to the elements of the mask has fallen out naturally in this development.
So far we have just used the library procedure convolve_2d to carry out the convolutions. How complex is such a procedure? In fact, a Pop-11 version is reasonably simple, and it would be a good exercise to try to write your own before looking at the one given below.
On first reading this teach file, you need not look at the following procedure in detail, and could skip to the next section. However, if you are writing your own vision programs, you should bear this example in mind. In particular, it is a very common mistake for people to write procedures like this with unnecessary assumptions built in - e.g. that the array bounds begin at 0 or 1, or that the (0, 0) point of the mask is in its centre. Such assumptions are bad practice (except in the rare cases where they allow a large efficiency gain) - procedures should be as general as possible. This convolution code illustrates how to write a general procedure that handles Pop-11 arrays properly, regardless of their boundslists.
define convolve_new(image, mask) -> result;
;;; This procedure carries out a convolution. Both the arguments
;;; must be 2-D arrays containing numbers. The result is a new
;;; 2-D array. The result bounds are chosen so that the whole of
;;; the output array can be filled without moving any mask
;;; element outside the bounds of image.
;;; Declare arguments as lvars for efficiency
lvars image, mask, result;
;;; Get the array bounds
lvars
(Icol0, Icol1, Irow0, Irow1) = explode(boundslist(image)),
(Mcol0, Mcol1, Mrow0, Mrow1) = explode(boundslist(mask));
;;; Set up the bounds for the results.
lvars
Rcol0 = Icol0 + Mcol1,
Rcol1 = Icol1 + Mcol0,
Rrow0 = Irow0 + Mrow1,
Rrow1 = Irow1 + Mrow0;
;;; Create the output array
newarray([% Rcol0, Rcol1, Rrow0, Rrow1 %]) -> result;
;;; Declare variables needed for the loops
lvars Rcol, Rrow, sum, Mcol, Mrow;
;;; Loop over the output array elements. Can use fast_for for
;;; a slight efficiency gain (does same as for)
fast_for Rrow from Rrow0 to Rrow1 do
fast_for Rcol from Rcol0 to Rcol1 do
0 -> sum; ;;; reset
;;; Loop over the mask elements, building up the sum
fast_for Mrow from Mrow0 to Mrow1 do
fast_for Mcol from Mcol0 to Mcol1 do
;;; Basic convolution formula
sum + mask(Mcol, Mrow) * image(Rcol-Mcol, Rrow-Mrow)
-> sum
endfor
endfor;
;;; Assign the complete sum to the result array
sum -> result(Rcol, Rrow)
endfor
endfor
enddefine;
You should be able to see how this procedure implements the calculation described in the first section above. The main things to notice are:
The last of these is the hardest part to get right in writing such a program - but the final formulae are surprisingly simple.
The techniques used in the procedure above are not restricted to Pop-11 - programs for this sort of operation are basically similar in most languages, except for special-purpose languages with built-in array operations or for use with parallel hardware. Pascal and FORTRAN procedures would look quite like the Pop-11 one, whilst C procedures are superficially rather different because C has a rather low-level view of arrays, though the underlying structure would be the same. (The curious can look at LIB *CONVOLVE_2D_F.C to see the C code called by convolve_2d.)
You can load the procedure defined above and check that it gives the same results as convolve_2d from the library. Assuming that mask has been set up as a mask array, you can compare the two displays resulting from
rci_show(convolve_2d(image, mask, false, false)) -> ;
rci_show(convolve_new(image, mask)) -> ;
which should look identical. However, there is one big difference - the library routine will run a lot faster than convolve_new. (Test this with *TIMEDIFF.) This is because convolve_2d uses externally loaded code written in C. The combination of code written in C for well-defined number crunching procedures such as convolution with code written in Pop-11 for higher-level processes and iteractive use (as in this teach file) is a powerful one.
The library procedure's last two arguments, which we have not used, provide added flexibility and efficiency for programs which use it. If you want to see what these arguments do, look at HELP *CONVOLVE_2D - you could consider incorporating the same features in any programs you write yourself.
As a final example of a convolution mask, we will look at the possibility of using a mask tailored to a specific feature for which we want to search. It seems intuitively likely that the convolution output will be highest at places where the image structure matches the mask structure, where large image values get multiplied by large mask values. We can try out this idea by picking out part of our image to use as a mask.
The *ARRAYSAMPLE library is convenient for this purpose. The following code copies a small part of the array into a new array - the part to be copied is specified by a boundslist-type argument:
arraysample(image, [98 108 128 138], false, [5 -5 5 -5], "nearest")
-> mask;
The 11 x 11 region we have copied, between columns 98 and 108 and rows 128 and 138, contains the oval image of the end of main pivot of the tripod head, as can be seen by looking at the mask with rci_show (increasing rci_show_scale temporarily if necessary). The other boundslist-type argument, [5 -5 5 -5], specifies that this region is to be copied onto columns 5 to -5 and rows 5 to -5 of a new array. The unconventional ordering in this list causes the rows and columns to be reversed when the values are copied (top to bottom and left to right) as required for a convolution template.
As it stands, this mask will not pick out any features - as all its values are positive, each output will be a weighted average of an 11 x 11 region of the input array, so the effect will just be smoothing. To make a useful feature detection mask, we need to have values that go negative as well as positive, so that the result will be zero for any uniform region of the input image. The following line of code does this by subtracting out the average of the values in the mask. (Refer to HELP *FLOAT_ARRAYPROCS if you want to use the routines yourself.)
float_addconst(-float_arraymean(mask), mask, mask) -> mask;
You can see that this has made the values go negative as well as positive with the simple numerical print routine from *SHOWARRAY:
3 -> sa_sigfigs; ;;; reduce the number of digits printed
sa_simple_nums(mask); ;;; print the whole array
prints:
-------------------------
5555544444333332222211111000001111122222333334444455555
-5> -40 -40 -40 -40 -27 32 74 68 -2 -40 -25
-4> -40 -40 -40 -40 -5 89 103 79 10 -40 -36
-3> -40 -40 -40 -38 60 107 94 64 -2 -40 -40
-2> -40 -40 -40 -6 66 66 38 28 -12 -40 -40
-1> -40 -40 -40 6 44 29 23 22 -4 -40 -40
0> -40 -40 -40 -5 50 10 4 4 3 -40 -40
1> -40 -40 -40 -2 71 49 69 82 46 -40 -39
2> -40 -40 -40 25 99 91 96 92 18 -40 -36
3> -40 -40 -40 -1 97 114 104 74 -20 -40 -29
4> -40 -40 -40 -39 74 131 105 27 -40 -40 -31
5> -40 -40 -37 -35 -26 -6 -37 -40 -40 -40 -24
Now you can display the result of convolving this mask, or template, with the original array, using
rci_show(convolve_2d(image, mask, false, false)) -> ;

Overall, the result looks pretty messy, because our mask happens to have a centre-surround structure and so is sensitive to much of the grey-level variation in the image. However, there is a definite bright patch at the position of the end of the pivot, and in fact the centre of this patch has the highest value in the output array (at row 103, column 133, as you can verify by writing a small program). In other words, the convolution operation has found the part of the image with the structure most closely corresponding to the template - not surprisingly, this is the part from which the template was originally copied.
The results of convolution processing are useful - the process is extremely common in both practical and experimental computer vision systems. However, the way in which the output of a convolution is actually handled in such systems has not been demonstrated here - rather convolution has been presented as an image processing operation, and the results presented graphically.
You should now:
and possibly:
Here are links to:
Copyright University of Sussex 1994. All rights reserved.