

Next: About this document
Bundle adjustment
Consider a situation in which a set of 3D points 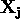 is
viewed by a set of cameras with matrices
is
viewed by a set of cameras with matrices 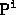 . Denote by
. Denote by 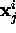 the coordinates of the j-th point as seen by the i-th
camera. We wish to solve the following reconstruction problem: given
the set of image coordinates
the coordinates of the j-th point as seen by the i-th
camera. We wish to solve the following reconstruction problem: given
the set of image coordinates 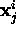 find the set of camera
matrices,
find the set of camera
matrices, 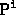 , and the points
, and the points 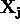 such that
such that
 . Without further restriction on
the
. Without further restriction on
the 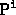 or
or  , such a reconstruction is a projective
reconstruction, because the points
, such a reconstruction is a projective
reconstruction, because the points  may differ by an arbitrary
3D projective transformation from the true reconstruction.
may differ by an arbitrary
3D projective transformation from the true reconstruction.
Bundle adjustment.
If the image measurements are noisy then the equations  will not be satisfied exactly. In this case we seek the
Maximum Likelihood (ML) solution assuming that the measurement noise is
Gaussian: we wish to estimate projection matrices
will not be satisfied exactly. In this case we seek the
Maximum Likelihood (ML) solution assuming that the measurement noise is
Gaussian: we wish to estimate projection matrices 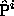 and 3D points
and 3D points 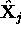 which project exactly to image points
which project exactly to image points
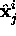 as
as 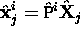 , and
also minimize the image distance between the reprojected point and
detected (measured) image points
, and
also minimize the image distance between the reprojected point and
detected (measured) image points 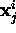 for every view in which
the 3D point appears, i.e.\
for every view in which
the 3D point appears, i.e.\
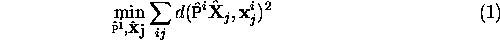
where 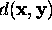 is the geometric image distance between
the homogeneous points
is the geometric image distance between
the homogeneous points  and
and 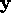 .
This estimation involving minimizing the reprojection error
is known as bundle adjustment -- it involves adjusting
the bundle of rays between each camera centre and the set of 3D points
(and equivalently between each 3D point and the set of camera centres).
.
This estimation involving minimizing the reprojection error
is known as bundle adjustment -- it involves adjusting
the bundle of rays between each camera centre and the set of 3D points
(and equivalently between each 3D point and the set of camera centres).
Bundle adjustment should generally be used as a final step of any
reconstruction algorithm. This method has the advantages of being
tolerant of missing data while providing a true ML estimate. At the
same time it allows assignment of individual covariances to each
measurement and may also be extended to include estimates of priors
and constraints on camera parameters or point positions.
In short, it would seem to be an ideal algorithm, except for the fact
that: (i) it requires a good initialization to be provided, and
(ii) it can become an extremely large minimization problem because of
the number of parameters involved. We will discuss briefly these two
points.
Iterative minimization.
Since each camera has
11 degrees of freedom and each 3-space point 3 degrees of freedom , a reconstruction
involving n points over m views requires minimization
over 3n + 11m parameters. In fact, since entities
are often over-parametrized (e.g. using 12 parameters
for the homogeneous 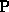 matrix) this may be a lower
bound. If the Levenberg--Marquardt algorithm is used
to minimize then matrices of
dimension
matrix) this may be a lower
bound. If the Levenberg--Marquardt algorithm is used
to minimize then matrices of
dimension 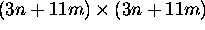 must be factored
(or sometimes inverted).
As m and n increase this becomes extremely costly,
and eventually impossible. There are several solutions
to this problem:
must be factored
(or sometimes inverted).
As m and n increase this becomes extremely costly,
and eventually impossible. There are several solutions
to this problem:
- Reduce n and/or m. Do not include all the views
or all the points, and fill these in later by resectioning or
triangulation respectively; or, partition the data into several sets,
bundle adjust each set separately and then merge.
- Interleave. Alternate minimizing reprojection error
by varying the cameras with minimizing reprojection error by varying
the points. Since each point is estimated independently given fixed
cameras, and similarly each camera is estimated independently from fixed
points, the largest matrix that must be inverted is the
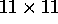 matrix used to estimate one camera.
Interleaving minimizes the same cost function as bundle adjustment,
so the same solution should be obtained provided it converges to a
global minimum,
but it may take longer to converge. Interleaving is compared with
bundle adjustment in
W. Triggs, P. F. McLauchlan, R. I. Hartley, and A. Fitzgibbon,
Bundle Adjustment for Structure from Motion.
in Vision Algorithms: Theory and Practice, Springer-Verlag, 2000.
matrix used to estimate one camera.
Interleaving minimizes the same cost function as bundle adjustment,
so the same solution should be obtained provided it converges to a
global minimum,
but it may take longer to converge. Interleaving is compared with
bundle adjustment in
W. Triggs, P. F. McLauchlan, R. I. Hartley, and A. Fitzgibbon,
Bundle Adjustment for Structure from Motion.
in Vision Algorithms: Theory and Practice, Springer-Verlag, 2000.
- Sparse methods.
Initial solution.
If the problem is restricted to affine cameras then
factorization gives a closed form optimal
solution provided points are imaged in every view. Even with projective
cameras there is an (iterative) factorization method
available provided points are imaged in
every view. If there is more information available on the data, for
example that it is partly coplanar, then again a closed form solution
is possible.
Finally, hierarchical methods
can be used
for the case
where points are not visible in every view.


Next: About this document
Bob Fisher
Thursday September 14 11:16:58 BST 2000
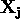 is
viewed by a set of cameras with matrices
is
viewed by a set of cameras with matrices 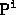 . Denote by
. Denote by 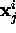 the coordinates of the j-th point as seen by the i-th
camera. We wish to solve the following reconstruction problem: given
the set of image coordinates
the coordinates of the j-th point as seen by the i-th
camera. We wish to solve the following reconstruction problem: given
the set of image coordinates 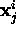 find the set of camera
matrices,
find the set of camera
matrices, 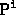 , and the points
, and the points 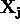 such that
such that
 . Without further restriction on
the
. Without further restriction on
the 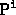 or
or  , such a reconstruction is a projective
reconstruction, because the points
, such a reconstruction is a projective
reconstruction, because the points  may differ by an arbitrary
3D projective transformation from the true reconstruction.
may differ by an arbitrary
3D projective transformation from the true reconstruction.


 will not be satisfied exactly. In this case we seek the
Maximum Likelihood (ML) solution assuming that the measurement noise is
Gaussian: we wish to estimate projection matrices
will not be satisfied exactly. In this case we seek the
Maximum Likelihood (ML) solution assuming that the measurement noise is
Gaussian: we wish to estimate projection matrices 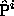 and 3D points
and 3D points 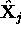 which project exactly to image points
which project exactly to image points
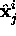 as
as 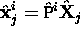 , and
also minimize the image distance between the reprojected point and
detected (measured) image points
, and
also minimize the image distance between the reprojected point and
detected (measured) image points 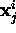 for every view in which
the 3D point appears, i.e.\
for every view in which
the 3D point appears, i.e.\
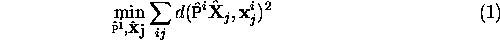
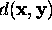 is the geometric image distance between
the homogeneous points
is the geometric image distance between
the homogeneous points  and
and 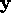 .
This estimation involving minimizing the reprojection error
is known as bundle adjustment -- it involves adjusting
the bundle of rays between each camera centre and the set of 3D points
(and equivalently between each 3D point and the set of camera centres).
.
This estimation involving minimizing the reprojection error
is known as bundle adjustment -- it involves adjusting
the bundle of rays between each camera centre and the set of 3D points
(and equivalently between each 3D point and the set of camera centres).
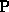 matrix) this may be a lower
bound. If the Levenberg--Marquardt algorithm is used
to minimize then matrices of
dimension
matrix) this may be a lower
bound. If the Levenberg--Marquardt algorithm is used
to minimize then matrices of
dimension 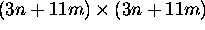 must be factored
(or sometimes inverted).
As m and n increase this becomes extremely costly,
and eventually impossible. There are several solutions
to this problem:
must be factored
(or sometimes inverted).
As m and n increase this becomes extremely costly,
and eventually impossible. There are several solutions
to this problem:
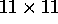 matrix used to estimate one camera.
Interleaving minimizes the same cost function as bundle adjustment,
so the same solution should be obtained provided it converges to a
global minimum,
but it may take longer to converge. Interleaving is compared with
bundle adjustment in
W. Triggs, P. F. McLauchlan, R. I. Hartley, and A. Fitzgibbon,
Bundle Adjustment for Structure from Motion.
in Vision Algorithms: Theory and Practice, Springer-Verlag, 2000.
matrix used to estimate one camera.
Interleaving minimizes the same cost function as bundle adjustment,
so the same solution should be obtained provided it converges to a
global minimum,
but it may take longer to converge. Interleaving is compared with
bundle adjustment in
W. Triggs, P. F. McLauchlan, R. I. Hartley, and A. Fitzgibbon,
Bundle Adjustment for Structure from Motion.
in Vision Algorithms: Theory and Practice, Springer-Verlag, 2000.