




Common Names: Mean filtering, Smoothing, Averaging, Box filtering
Mean filtering is a simple, intuitive and easy to implement method of
 smoothing images, i.e. reducing the amount of intensity variation
between one pixel and the next. It is often used
to
smoothing images, i.e. reducing the amount of intensity variation
between one pixel and the next. It is often used
to  reduce noise in images.
reduce noise in images.
The idea of mean filtering is simply to replace each pixel value in an
image with the mean (`average') value of its neighbors, including
itself. This has the effect of eliminating pixel values which are
unrepresentative of their surroundings. Mean filtering is usually
thought of as a
 convolution filter.
Like other convolutions it is based around a kernel, which
represents the shape and size of the neighborhood to be sampled when
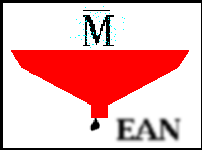
calculating the mean. Often a 3×3 square kernel is used, as
shown in Figure 1, although larger kernels (e.g. 5×5
squares) can be used for more severe smoothing. (Note that a small
kernel can be applied more than once in order to produce a similar
but not identical effect as a single pass with a large kernel.)
convolution filter.
Like other convolutions it is based around a kernel, which
represents the shape and size of the neighborhood to be sampled when
calculating the mean. Often a 3×3 square kernel is used, as
shown in Figure 1, although larger kernels (e.g. 5×5
squares) can be used for more severe smoothing. (Note that a small
kernel can be applied more than once in order to produce a similar
but not identical effect as a single pass with a large kernel.)
Figure 1 3×3 averaging kernel often used in mean filtering
Computing the straightforward convolution of an image with this kernel carries out the mean filtering process.
Mean filtering is most commonly used as a simple method for reducing noise in an image.
We illustrate the filter using
The image
shows the original corrupted by Gaussian
noise with a mean of zero and a standard deviation (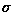 ) of 8.
) of 8.
The image
shows the effect of applying a 3×3 mean filter. Note that the noise is less apparent, but the image has been `softened'. If we increase the size of the mean filter to 5×5, we obtain an image with less noise and less high frequency detail, as shown in
The same image more severely corrupted by Gaussian noise (with a mean
of zero and a 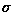 of 13) is shown in
of 13) is shown in
The image
is the result of mean filtering with a 3×3 kernel.
An even more challenging task is provided by
. It shows an image containing `salt and pepper' shot noise.
The image
shows the effect of smoothing the noisy image with a 3×3 mean filter. Since the shot noise pixel values are often very different from the surrounding values, they tend to significantly distort the pixel average calculated by the mean filter.
Using a 5×5 filter instead gives
This result is not a significant improvement in noise reduction and, furthermore, the image is now very blurred.
These examples illustrate the two main problems with mean filtering, which are:
Both of these problems are tackled by the median filter, which is often a better filter for reducing noise than the mean filter, but it takes longer to compute.
In general the mean filter acts as a  lowpass frequency filter
and, therefore, reduces the spatial intensity derivatives
present in the image. We have already seen this effect as a
`softening' of the facial features in the above example. Now consider
the image
lowpass frequency filter
and, therefore, reduces the spatial intensity derivatives
present in the image. We have already seen this effect as a
`softening' of the facial features in the above example. Now consider
the image
which depicts a scene containing a wider range of different spatial frequencies. After smoothing once with a 3×3 mean filter we obtain
Notice that the low spatial frequency information in the background has not been affected significantly by filtering, but the (once crisp) edges of the foreground subject have been appreciably smoothed. After filtering with a 7×7 filter, we obtain an even more dramatic illustration of this phenomenon in
Compare this result to that obtained by passing a 3×3 filter over the original image three times in
Variations on the mean smoothing filter discussed here include
 Threshold Averaging wherein smoothing is applied subject to the
condition that the center pixel value is changed only if the
difference between its original value and the average value is greater
than a preset threshold. This has the effect that noise is smoothed
with a less dramatic loss in image detail.
Threshold Averaging wherein smoothing is applied subject to the
condition that the center pixel value is changed only if the
difference between its original value and the average value is greater
than a preset threshold. This has the effect that noise is smoothed
with a less dramatic loss in image detail.
Other convolution filters that do not calculate the mean of a neighborhood are also often used for smoothing. One of the most common of these is the Gaussian smoothing filter.
You can interactively experiment with this operator by clicking here.
and note the strength of the output. Then apply a 3×3 mean filter to the original image and run the edge detector again. Comment on the difference. What happens if a 5×5 or a 7×7 filter is used?
R. Boyle and R. Thomas Computer Vision: A First Course, Blackwell Scientific Publications, 1988, pp 32 - 34.
E. Davies Machine Vision: Theory, Algorithms and Practicalities, Academic Press, 1990, Chap. 3.
D. Vernon Machine Vision, Prentice-Hall, 1991, Chap. 4.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.


