|
|
|
|
We have compared the performance of neural networks trained with two Bayesian methods, (i) the Evidence Framework of MacKay (1992) and (ii) a Markov Chain Monte Carlo method due to R. Neal (1996) on a task of classifying segmented outdoor images. In order to quantify how much the performance of a neural network is affected by the amount of training data, we have we conducted experiments reducing the number of data points in the training sets.
A neural network with an hidden layer with 30 units has been trained with both the Bayesian techniques.
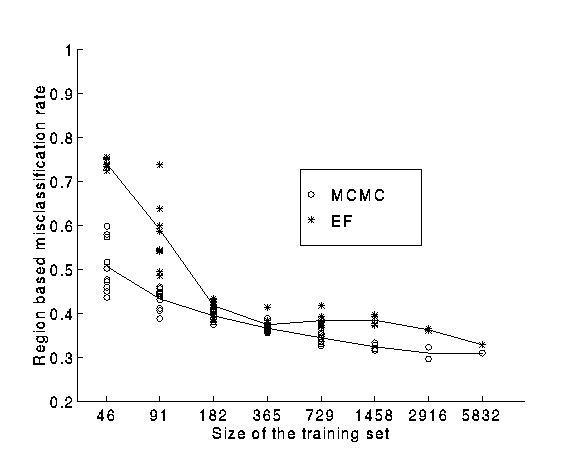
Plot of the learning curves for the EF and MCMC methods
obtained
by reducing the number of data points in the training sets.
The figure shows the plots of the misclassification as a function of the number of training data.
For both the methods each point of the plot corresponds to a different training set. We used 2 training sets with 2916 data, 4 with 1458, 8 with 729 and 10 training sets with each of 365, 182, 91, and 46 data points.
Our results suggest that on this task using large amounts of training data the evidence framework and Markov Chain Monte Carlo performance is similar, but that the MCMC method seems superior on smaller-sized training sets.
A paired 2-sided t-test finds that the differences between EF and MCMC are statistically significant at the p < 0.05 level for training set sizes 1458, 729, 182, 91 and 46.
The results presented in this web page have been published in the paper Using Bayesian Neural Networks to Classify segmented Images which is available as compressed postscript .
| Project Home page | Introduction | Work plan | Publications |