Combining Spatially-Distributed Predictions from Neural Networks
EPSRC grant GR/L 03088
PI: Dr Chris Williams Division of Informatics, University of Edinburgh
CI: Dr Ian Nabney, EECS Division, Aston University
Grant duration: March 1997-March 1999
Report date: June 1999
Our aim in this project was to develop theory for the use of neural network
predictions in spatially-distributed problems, and to implement this theory
in application areas. Two application areas have been investigated
intensively, namely the reconstruction of wind-fields from radar
scatterometer data, and image segmentation.
In general we wish to carry out inference for some variables 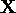 given some data
given some data  . For example
. For example  may represent wind vectors at a grid of locations, and
may represent wind vectors at a grid of locations, and
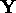 would be satellite
observations at the same locations. At each spatial location i
neural networks can be trained to output an estimate of
would be satellite
observations at the same locations. At each spatial location i
neural networks can be trained to output an estimate of 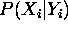 , and these can be converted into
scaled likelihoods using
, and these can be converted into
scaled likelihoods using 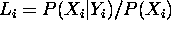 . Under the assumption that
. Under the assumption that 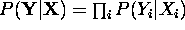 these scaled likelihoods can be combined with a prior
model
these scaled likelihoods can be combined with a prior
model 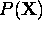 to obtain the posterior
distribution
to obtain the posterior
distribution 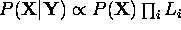 , see [1].
, see [1].
We have applied this method to two main problems. The first of these
is an image segmentation task, where we wish to assign labels (e.g.
``road'', ``sky'', etc) to each pixel in an image. Here we built
a tree-structured belief network (TSBN) model of the label images. This
was trained using both maximum likelihood methods (using the EM
algorithm) and conditional maximum likelihood methods. These TSBN
models were evaluated as coding models of label images, and gave
superior performance compared to block coding methods. The TSBN prior
was combined with scaled likelihoods from neural networks to make
predictions at each pixel. See refs [5] [6] [7] [8] for more details.
This research also led to the development
of novel ``dynamic trees'' models of images, which are TSBN models which
can adapt their architecture in response to an input image [9] [10].
The second application was in wind-field modelling. We developed
Gaussian-process prior models of wind fields. Because these models can
be too smooth if there are frontal features in the wind field, we
developed Gaussian process models with constrained discontinuities to
model these situations. The prior models were fused with neural
network predictions to obtain posterior estimates of the entire wind
field. This method has been evaluated extensively on operational
data (over 300 scenes), and produced significantly more accurate
results approximately six times faster than the current operational
methods. Our method is now being considered for use in day-to-day
operations [2] [3] [4]. For more information on wind-field modelling and
fusion with scatterometer data, follow this link, and see especially the work
on ambiguity removal.
Acknowledgements
This work was funded by EPSRC grant GR/L03088, Combining Spatially
Distributed Predictions From Neural Networks. We gratefully
acknowledge the assistance of British Aerospace and the Meteorological
Office in the work on image segmentation and wind-field analysis
respectively.
Publications arising from this work
[1] NCRG/97/026 Combining spatially distributed predictions from neural networks. C. K. I. Williams.
Technical Report, Neural Computing Research Group, Aston University, 1997.
[2] NCRG/98/023 Bayesian Inference for Wind Field Retrieval
I T Nabney, D Cornford, and C K I Williams.
Neurocomputing Letters, 26-27:1013--1018, 1999.
[3] NCRG/98/025
Adding Constrained Discontinuities to Gaussian Process Models of
Wind Fields
D. Cornford, I. T. Nabney, and C. K. I. Williams.
In M. J. Kearns, S. A. Solla, and D. A. Cohn, editors, Advances
in Neural Information Processing Systems 11. MIT Press, 1999.
[4] NCRG/99/001
Modelling frontal discontinuities in wind fields.
D. Cornford, I. T. Nabney, and C. K. I. Williams.
Technical Report, Neural Computing Research Group, Aston University, 1999.
[5] NCRG/98/013 Combining neural networks and belief networks for image segmentation
C. K. I. Williams and X. Feng.
In T. Constantinides, S-Y. Kung, M. Niranjan, and E. Wilson, editors,
Neural Networks for Signal Processing VIII. IEEE, 1998.
[6] NCRG/98/014 Training Bayesian networks for image segmentation
Xiaojuan Feng and C. K. I. Williams.
In F. Preteux, J. L. Davidson, and E. R. Dougherty, editors,
Mathematical Modeling and Estimation Techniques in Computer Vision ,
volume 3457, pages 82--92. SPIE, 1998.
[7] Combining belief networks and neural networks for image segmentation
gzipped postscript
Xiaojuan Feng and C. K. I. Williams. 1999
Submitted to IEEE Trans. PAMI.
[8] Tree-structured Belief Networks as Models of Images.
gzipped postscript
Xiaojuan Feng and C. K. I. Williams. 1999
To appear in Proc. ICANN'99. IEE, 1999.
[9] DTs: Dynamic Trees
gzipped postscript
C. K. I. Williams and N. J. Adams.
In M. J. Kearns, S. A. Solla, and D. A. Cohn, editors, Advances
in Neural Information Processing Systems 11. MIT Press, 1999.
[10] SDTs: Sparse Dynamic Trees. N. J. Adams and C. K. I. Williams.
To appear in Proc. ICANN'99. IEE, 1999.
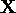 given some data
given some data  . For example
. For example  may represent wind vectors at a grid of locations, and
may represent wind vectors at a grid of locations, and
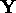 would be satellite
observations at the same locations. At each spatial location i
neural networks can be trained to output an estimate of
would be satellite
observations at the same locations. At each spatial location i
neural networks can be trained to output an estimate of 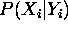 , and these can be converted into
scaled likelihoods using
, and these can be converted into
scaled likelihoods using 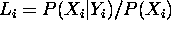 . Under the assumption that
. Under the assumption that 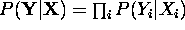 these scaled likelihoods can be combined with a prior
model
these scaled likelihoods can be combined with a prior
model 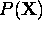 to obtain the posterior
distribution
to obtain the posterior
distribution 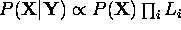 , see [1].
, see [1].