University of Edinburgh

Department of Computer Science

 

 

 

A tool for investigating
type errors in ML programs

MSc Project Report

Alison Keane

14 September 1999

 

 

 

Abstract

 

This project aims to produce a tool to aid in the processes of identifying and correcting types errors in ML. Specifically, it will (1) allow the type of an expression or part of an expression to be determined and (2) allow a type to be assumed for an expression and the resultant state examined/investigated. The implementation of these goals should provide a ‘point & click’ style approach to type debugging for ML.

Acknowledgements

I would like to thank my supervisor Don Sannella for all his guidance and assistance with this project.

I am very grateful to my family for their help and support.

Thanks to Bruce Mc Adam for his help in locating relevant papers.

 

Contents

Chapter 1 Introduction *

1.1 Project description *

1.1.1 Show type for expression *

1.1.2 Assume type for expression *

1.2 Approaches taken to identify errors while typechecking *

1.2.1 Modifying unification algorithm; tracking type inferences *

1.2.2 Modifying type inference algorithm; order of substitution *

1.2.3 Visualisation of typechecking *

1.2.4 Identifying place of error *

1.2.5 Extra type information *

1.3 This project *

Chapter 2 Typechecking *

2.1 Type inference *

2.2 Types & Type Environments *

2.2.1 Type variables *

2.2.2 Generic and non-generic type variables *

2.3 Unification *

2.3.1 Example of unification *

2.3.2 Most general unifier *

2.3.3 Unification Algorithm *

2.4 Typechecking algorithm *

Chapter 3 Language used *

3.1 ML and the kit compiler *

3.2 Source of language; Cardelli *

3.3 Language extensions *

3.4 Parsing the language *

Chapter 4 Typechecking *

4.1 Data structures *

4.2 Typechecking *

4.2.1 Unification failure *

4.2.2 Dealing with errors *

4.2.3 Propagating errors *

4.2.4 Error reported *

4.3 Extensions *

4.3.1 Constants *

4.3.2 Tuples *

4.3.3 Datatypes *

4.3.4 Pattern matching *

4.3.5 Derived expressions *

4.3.6 Exceptions *

4.3.7 Eqtypes *

4.3.8 Overloaded Operators *

Chapter 5 Goal 1: Find type of expression *

5.1 Identifying the type *

5.2 Identifying the expression *

5.3 Example *

Chapter 6 Goal 2: Assume type for expression; first approach *

6.1 Localised re-typechecking *

6.2 Advantages *

6.3 Problems *

Chapter 7 Goal2 : Assume type for expression; second approach *

7.1 Possible strategies *

7.1.1 Re-typechecking from the beginning *

7.1.2 Using the tree already present *

7.2 Overview of the approach *

7.3 Implementation decisions *

7.3.1 Recording the results of changes *

7.3.2 Inside an assumed expression *

7.3.3 Conflicting assumptions *

7.3.4 Effect on terms within expression *

7.4 Features *

7.4.1 Let-bound variables *

7.4.2 Lambda bound variables inside of a function *

7.4.3 Sequence of changes *

7.5 Focussing in on error terms *

7.5.1 Solution *

7.5.2 Finding the types of expressions inside a focus *

7.5.3 Changing the types of expressions inside a focus *

Chapter 8 Goal 2: Assuming polymorphic types *

8.1 The problem *

8.2 The solution *

8.2.1 The steps *

8.3 Example *

8.4 User supplied polymorphic types *

8.4.1 The problem *

8.4.2 Solution *

8.4.3 Example *

Chapter 9 User Interface *

9.1 Requirements *

9.2 Java *

9.3 The main window *

Chapter 10 Case study example *

Chapter 11 Summary and conclusions *

11.1 Realisation of goals *

11.2 Extensions *

11.2.1 Extending for ML *

11.2.2 ML kit compiler *

11.2.3 Improved error messages *

11.2.4 User interface *

11.3 Conclusion *

Appendix A Language *

Appendix B Inference Rules *

Bibliography *

 

  1. Introduction

    1. Project description

      2. The goal of this project is to produce a tool that will help with the investigation of type errors in ML or a similar language, which supports polymorphism. Sometimes type related errors in ML can be sparse and confusing. This is a feature of polymorphic typechecking. Because of polymorphism a user error can result in a type being inferred where an error should ideally have been reported. When this erroneous type is used it can result in confusing and misleading error messages. Obviously, reporting the source of such an error can be difficult.

      ML is itself the typechecker. When a problem is encountered it will usually try to highlight the position in the code where the problem has occurred. However this position may be where the type clash was discovered, not where the problem was introduced. For example, a definition might result in type A when the programmer was expecting type B. When this definition is used the programmer will use it as type B. The typechecker will see it as type A and report an error. This error however is not with the use of the definition but with the definition itself.

      In the above situation it becomes necessary to refer back to the type the compiler has assigned to the various expressions to try to discover the cause of the problem. A further complication is that in the case of the let statement the compiler does not report the types of the declarations inside the let statement.

       

      1. Show type for expression

        2. The debugging process would be made simpler if the type of an expression could be obtained immediately from the typechecker. This is the first aim of this project: to produce a tool that will obtain the type for an expression or part thereof.

        This goal will lead to a powerful interactive tool that can be used to facilitate the debugging and typechecking of ML code.

      2. Assume type for expression

      The second aim of the project is to allow the user to change the type of various expressions and see what happens as a result. To achieve this currently using ML a programmer would have to enter a cycle of applying changes to the source code and observing the results. This can be tedious and laborious and leads to the alteration of the original code.

      If, however, the type of an expression could be assigned manually, the overall effect of the change could be examined very quickly and easily. If, for example a programmer thinks that an expression should be of type1 but the system reports it as type2 he can set it to type1 and allow the typechecking to continue. This will allow the programmer to zero in on the source of the error.

      Furthermore, the majority of ML environments stop checking when a problem has been encountered. As a result the remainder of the program cannot be typechecked. By assuming a type for a particular problematic part of the program the remainder of the program can be typechecked and the problem corrected afterwards.

    2. Approaches taken to identify errors while typechecking

      3. A significant amount of work has been done in an attempt to debug type errors. Some of the various approaches taken are described below.

       

      1. Modifying unification algorithm; tracking type inferences

        2. In Duggan & Bent [DB96] a modification to the unification algorithm is presented that allows the specific reasoning which lead to the program variable having a particular type to be recorded. This information can then be used to generate a type explanation for particular variables.

        This approach was thought to closely resemble the intuitive process generally used for debugging type errors.

      2. Modifying type inference algorithm; order of substitution

        3. Another approach, taken by McAdam in [McA98b], involved modifying the type inference algorithm to delay the application of substitutions. The idea behind this approach is to reduce the bias of detecting errors towards the end of the program.

        As a result errors should be identified closer to the source of the problem.

         

      3. Visualisation of typechecking

        4. Jun & Michaelson [JM97] provide a visualisation of polymorphic typechecking. They deal with functions where the types of the function domains and codomains are represented graphically. As the functions are applied and used, the graphical types change dynamically.

        The idea here is that type clashes should be identified by clashes in the graphical representation.

      4. Identifying place of error

        5. Wand [Wan86] believed that errors are usually reported some distance from where they actually originate. He presented an algorithm which attempts to identify the place where the error occurs rather when where it is detected.

        This is done by supplying a number of possible error sites when an error is detected. One of these error sites should be the real error.

      5. Extra type information

      Bernstein and Stark [BS95] try to supply extra type information. This is achieved by allowing an extended type definition that assigns types to open expressions as well as closed ones. . By allowing the open expressions (expressions containing free variables) to have a type they can be used in appropriate places to gather type information and then this type information can be displayed with the error that will result from the open expression.

      This method allows the programmer to extract information from inside the program by inserting an open expression in an appropriate place and then looking at the error information. When it is not needed this method is unobtrusive.

       

    3. This project

    The work described in section 1.2 has been carried out in an attempt to develop a more informative typechecking environment for a user and to help to them discover the source of the type error more easily.

    In this project, no attempt is made to explain the type inference process as in [DB97] or to identify the true source of the error as in [Wan86]. The process of trying to find the source of the error is left in the hands of the user. What is done is to try and supply more type information about the expressions. However, unlike [BS95] it is not necessary to insert dummy variables in the appropriate place to achieve this aim. Because of the "point & click" interface a large amount of information is available but at no point is the user overwhelmed by the information available.

    The other aspect of the project that involves changing the types means that the user can further investigate the type error. If it is not clear where the error lies this "changing the type facility" can be used to home in on the error.

    This project should provide a useful and easy to use tool to investigate the cause of type errors.

     

  2. Typechecking

    3. This chapter contains an overview of typechecking and the various processes therein that are relevant to this project. In many cases the types resulting from expressions used in programming languages will not be obvious. This might be because of the complex structure of the expression or the use of user-defined types. This lack of visibility can often lead to errors.

    1. Type inference

      2. Type inference is the compile time process of reconstructing missing type information in a program based on the usage of its variables. Consider:

      fn x Þ x + 1

      As a result of the addition operation the x is constrained to be of type int. As a result the function will be of type: int ® int.

      The type inference system in ML means that, except for a few exceptional cases, the programmer does not need to supply any types as they are automatically inferred by the system. In the above example the programmer does not need to explicitly declare that the function is of type int ®  int.

      A type inference system depends on a series of type rules. For example, consider the following type inference rule

      The way in which this inference rule is interpreted is as follows. If an expression is of the form if then else then the type of this expression is determined by looking at the two branches of the conditional. If the type of x and y evaluate to the same type t (or can be unified to the same type, see Section 2.3) then the type of the whole if then else expression is this type t . The other rule states that the type of the condition x must be of bool type. All of these types are evaluated in the type environment E.

       

      These type inference rules provide a set of constraints which must be solved in order to find the type of an expression.

    2. Types & Type Environments

A type can be either:

For example, basic types such as int, bool etc. are type operators with no arguments. A list is a type operator with just one argument. ® and * are type operators with two arguments.

 

A type environment can be considered as a mapping between identifiers and type schemes. It is of the form

TE =

 

A type scheme is a universally quantified type. e.g. . What this means is that any type variables quantified are non-generic whereas any free type variables are generic. (Generic and non-generic type variables are described in Section 2.2.2.)

      1. Type variables

        2. A type variable, a , b etc. stands for an arbitrary type. The type variables in an expression can be replaced by arbitrary types to give a more specialized type for that expression. Multiple occurrences of a type variable in a type expression illustrate the dependencies between types. When a type variable is instantiated, the other occurrences of the same variable must be set to the same value.

        For example the function

        a * b ® a

        can be legally instantiated by

        int * string ® int , or
        (string *string ) * int ® string * string.
        (t ® bool) * real ® (t ® bool)

        An example of an illegal instantiation would be

        int * bool ® bool

        as it would be necessary to instantiate the a to bool and int.

      2. Generic and non-generic type variables

Type variables appearing in the type of a lambda bound identifier are called non-generic. The reason for this is that they are shared by every occurrence of the variable in the function body. Consider the case

fun f (x) = ( f (3) , f (true) )

The first use of f requires it to have type int ® 'a. The second instance requires it to have type bool ® 'a. Because in this instance the 'a is non-generic, this gives rise to a conflict as the type int can't be unified with the type bool.

But suppose f is introduced through a let. For example,

let f = fn (x) = x in (f(2) , f(true))

This example will typecheck correctly because inside of the body of the let each f is a separate instance. (The type variables in f here are generic). In the first case f can be set to int ® ‘a and in the second instance it can be set to bool ®  'b, and so no conflict arises.

As described above, non-generic type variables are those type variables that are quantified in a type scheme whereas generic type variables are those free type variables in the type scheme; more information is available in [FH88].

    1. Unification

      2. In certain instances of the type inference rules, the requirement is that the type of the overall expression is the type of some other expressions. For example consider the following:

      In this instance y and z must have the same type. To ensure this happens a process called unification needs to be applied to the types of y and z.

      If the unification of two type expressions is successful, it produces a substitution involving the type variables in the two expressions. On application of this substitution to the two expressions being unified, the result is the same type expression. Moreover that type expression is the most general common instance of the original expressions. When two expressions fail to unify a type error is raised.

      1. Example of unification

        2. For example, consider the unification of

        ‘a ® int ® int
        with

        bool ® ‘b ® int

        The substitution that is produced as a result of the unification is { [bool / ‘a], [int / ‘b] }.

        On the other hand, the following two types

        ‘a ® int ® bool

        and

        bool ® ‘b ® ‘b

        will fail to unify. A successful unification would require that ‘b would be mapped to both int and bool, which is not allowed.

      2. Most general unifier

        3. The unification algorithm guarantees the most general unifier. To explain this consider the unification of the following two types:

        ‘a ® ‘b

        and

        int ® ‘b

        A number of substitutions are valid: { [int / ’a] }, { [int / ‘a], [int / ‘b] }, { [int / ‘a], [int * int / ‘b] }, { [int / ‘a], [string * string / ‘b] } etc. There are any number of possible substitutions that will make the two expressions equal.

        However the unification algorithm guarantees to return the most general unifier. So in this case this is the one that does not constrain ‘b at all i.e. { [int / ’a] }. This result is guaranteed by Theorem 7.1 (Robinson, 1965) in [FH88]

      3. Unification Algorithm

      The unification algorithm that is used can be described as follows:

      Unify T1 T2

      type T1

      Type T2

      Action required
       

      a

      a

      No action required. The types are identical
       

      a

      W n, args

      If Occurs(a , W n, args) then Fail.
      Otherwise a is instantiated to W n, args.
       

      W n, args

      a

      Unify T2 T1
       

      W m, args

      W n, args’

      If W m=W n then UnArgs(args, args’). Otherwise Fail.
             

      UnArgs I1 I2

      []

      []

      No action required. No types to match.
       

      h::t

      h’::t’

      ( Unify h h’ ; UnArgs t t’ )
       

      -

      -

      Fail

      In the above tables a identifies type variables and W n, args type operators.

      Occurs(a , W n, args) checks whether the type variable occurs anywhere in the arguments of the operator. If it does then there is a possibility of a cyclic substitution, which could cause the unification algorithm to loop infinitely. To avoid this unification stops when this occurs.

    2. Typechecking algorithm

The algorithm that deals with typechecking is called Algorithm W. A formal description is provided in [Mil78]. An informal description is supplied here, based on the description in [Car87]

If a new variable x is introduced by a lambda binder, it is assigned a new type 'a which means that its type must be further determined by the context of its occurrences. The pair consisting of x and its type 'a is stored in an environment. This environment is then searched every time an occurrence of x is found, and returns 'a (or it's current instantiation) as the type of that occurrence.

If it is a conditional, then the type of the condition must be unified with bool. Then the then and else branches are unified to determine a unique type for the whole if then else expression

If it is a lambda abstraction of the form fun(x) e, the type of e is inferred in a context where the x has been associated with a new type variable. The return type is of the form 'a (or it's current instantiation) ® 'b, where 'b is the type of e.

If it is an application of the form f(y), the type of f is unified with the type 'a ® b where 'a is the type of y and b is a new type variable. So f must be a function type whose domain can be unified with the type of y. The type b (or any instantiation of it) is the type that will be returned as the type of the whole application.

If it is a let, then the declaration part of the let is typechecked to provide an environment. This environment is then used when typechecking the of the let.

If it is a declaration then each of its definition are dealt with as follows. A definition of the form x = t has the effect of introducing the pair <x,T> into the environment where T is the type of t. If x is a recursive definition then the pair <x,a > is introduced into the environment. Then t is typechecked and its type t is matched with a .

 

  1. Language used

    2. This chapter describes the language used for the purpose of this project.

    1. ML and the kit compiler

ML is referred to in the title of this project. If ML was used as the language for this project then, because of the size of the language and the difficulty of parsing it correctly, it would have been necessary to extend an existing ML compiler to improve the typechecking algorithm and provide the new functionality required for this project.

The ML kit compiler [BRTT93] is a compiler for ML that is written in ML. Extending this kit compiler seemed to offer the following advantages:

However, the following disadvantages were soon realised:

As a result of these disadvantages it was decided that the kit compiler would not be used.

    1. Source of language; Cardelli

      2. Having made the decision not to use the ML kit compiler a replacement language was needed. Furthermore a parsing and typechecking engine for the replacement language would be needed. Java was chosen as the implementation language (see Chapter 9).

      Creating a typechecking engine from scratch would have used up a significant part of the time available for this project. To avoid this necessity the project is based on the typechecker provided by Cardelli in [CAR87]. This typechecker deals with a small subset of the ML core language.

      The language is described by

      Exp ::=

      Identifier|
      'if' Exp 'then' Exp 'else' Exp |
      'fn' Identifier 'Þ ' Exp |
      Exp '(' Exp ')' |
      'let' Decl 'in' Exp |
      '(' Exp ')'

      Decl::=

      Ide'='Exp|
      Decl 'then' Decl |
      'rec' Decl |
      '(' Decl ')'

      The language contains lambda abstractions, let expressions and also recursion. A number of extensions were introduced to cover a larger subset of ML. These are described in the next section. The type inference rules for this small language are given in Appendix B.

    2. Language extensions

The following features were added to the language to make it more realistic for the purposes of the project:

The full syntax of the extended language is given in Appendix A.

    1. Parsing the language

A recursive descent parser had to be written to translate the source program into a tree structure. The nodes in the tree are decorated with additional information that will be populated as part of the parsing process and further populated as part of the typechecking process.

The details of the structure of the nodes are described in the following section. The parsing algorithm is available in the Java source code written for this project.

  1. Typechecking

    2. This chapter describes the workings of the typechecker. This understanding is necessary because it is at this stage that the information required to realise the project goals is derived and generated.

    1. Data structures

      2. A tree structure is used to hold the parsed program. It consists of a number of nodes of the following structure:

       

      Information for original program

      Nature of node e.g. expression, constant etc.

      Type (if typechecked correctly)

      Any unification error that occurred at this node

      Positional information for node in original code

      Links to child nodes

      Information for assuming types

      Working value for type

      Any assumed type

      Unification errors resulting from type assumption

      For each identifier the original type is stored

       

    2. Typechecking

The base typechecker was taken from Cardelli’s paper [CAR87]. However this had to be modified extensively for a number of reasons:

  1. The implementation language for this project is Java.

  2. The language being typechecked had been extended to include data types and pattern matching.

  3. More detailed error handling was required.

      1. Unification failure

        2. There are two things that can be done when unification fails and a type error occurs. Normally typechecking ceases, an exception is raised and the unification error is reported. However in this case we want as much information as possible to be available to the user, so that they can try to discover the cause of the type error. Therefore when a unification error occurs typechecking continues.

        Consequently there may be more than one error in an expression. To facilitate the tracking of the errors and their reporting to a user the errors are stored in the nodes at which they occur – as opposed to a flat list of errors available at the end of the process.

        Consider the following example,

        if pred (true) then succ (false) else pred (1)

        This results in the following tree:

         

         

        Unification produces an error at the application of pred to true; this error state is stored in the node. The unification process then continues onto the then branch and fails at the application of succ to false. The error is once again stored in the succ node. Once again unification continues and produces an int type for the final pred node. However the unification for the complete if – then – else expression will not be carried out and an error will be recorded.

        To try and get as much information as possible without the terms that fail to unify affecting anywhere else a method described in [Hay93] has been followed: before two expressions are unified, a copy of them is made. Then these two copies are unified. If they unify successfully then the originals are unified and typechecking continues.

        If unification is not successful, details of the unification error are stored and no further unification is carried out in that expression to try and prevent incorrect information being stored about the types. Consequently any parts of the tree that typecheck correctly will have valid type information stored in the nodes and these will not be affected as a result of a type error occurring during the typechecking of another expression.

        Consider the following example,

        fn (x,y,z) Þ (if true then (x, y, y) else (5, "sd", 6)

        Before any unification occurs between the two tuples, x will have type a , y will have type b and z will have type c . The x will be instantiated to int and the y will be unified with string. As a result, when an attempt is made to unify y with int a type error will occur. Effectively what happens here is that the type variables will revert back to the original state that existed before this erroneous unification started.

        So the variables will now have the following types:

        x : a
        y : b
        z : c

        This is the state that existed before any unification took place for the if – then – else expression.

      2. Dealing with errors

        3. In the case of a let bound declaration, if an error occurs in the declaration part of it then anywhere its used needs to be marked with an error. For this purpose a list of the declarations containing errors is retained. When a reference is made to any of the identifiers contained in the list the particular instance is marked with an error. This allows correct expressions elsewhere in let declarations to be typechecked and ones that use the incorrect declarations to be marked with an error.

        However there is a problem with recursive types. These are handled as follows. If a recursive function typechecks incorrectly then the whole function is marked as containing an error and any expression using it is defined as having an error. However inside of the recursive function , if the function calls itself then this recursive call won't be marked with an error. To try and do this would involve typechecking it once and then re-typechecking marking any call on this declaration as an error and then propagating the error the whole way through the declaration. This would be a bit laborious and has not been done. As long as the whole function is marked with an error then any other expression that calls on it will also be marked with an error except for inside the function itself.

      3. Propagating errors

        4. There are two different types of errors that can occur.

        The first type of error is a direct result of the unification process. For example in an if then else if the error occurred in trying to unify the then and else parts then details of the unification error that occurred would be given in the error description.

        The second type of error occurs when one of the sub-expressions in the expression has an error (of either type). When any of the sub-expressions have an error then the expression containing it must also have a type error i.e. the error is propagated up the tree. This sort of error is a direct result of continuing to typecheck after a unification error.

        For example in an if then else, if an error occurred in the condition part, then the whole expression would be marked as having an error. However the description of the error will only indicate that there is an error inside the expression. This may seem a bit uninformative, however the user will be able to investigate the types of the terms inside the expression to try and locate the term containing the error.

        It seemed sensible to distinguish between the two types of errors. If for example the error occurs in one branch of an if then else and a report indicates that the whole expression has the type error, then it might just confuse the user as to the true position of the error. They might think a problem occurred when trying to unify the two branches of if then else.

        Consider the following example,

        fn(y) Þ if true then 1 else "-"

        This will lead to the following tree structure.

      4. Error reported

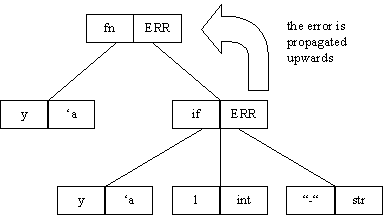
As typechecking continues after an error has occurred, it is possible that more errors may be encountered before the whole typechecking process finishes. In this case it is the first and only the first error encountered that is reported. This is because most of the remaining errors will probably be a consequence of the first error. Reporting them all would mislead the user, as in most cases there is only one error that really needs to be dealt with.

 

    1. Extensions

      2. Some extensions were made to the typechecker.

      1. Constants

        2. In Cardelli's typechecker the datatype types are added to the environment in the beginning. So when a user starts the environment already contains true, false, nil, cons (and therefore the type constructor list) and some integers. This meant that for a constant to be identified it had to be present in the initial environment. In the case of the string type it is not feasible to enumerate all the possible string values. So it was decided to extend the typechecker to deal with constants.

        All the typechecker needs to do when it encounters a constant node is to return the type of that constant.

      2. Tuples

        3. Tuples were also added to the language. However all that was really added was a 2-tuple as all other tuples can be treated as 2-tuples.

        For example the type of

        ( 1 , "sdfsdf" , #"d" , true )

        is really

        (int * ( string * ( char * bool ) ) ).

      3. Datatypes

        4. The addition of datatypes was needed in order to provide realistic pattern matching. The declaration of datatypes in effect adds some more functions to the environment. For example the declaration of a list would be

        datatype 'a list = nil | cons of 'a * 'a list

        and this has the effect of adding the functions

        nil : 'a list
        and
        cons : 'a * 'a list ® 'a list

        to the environment. However while these can be used as normal functions they can also be used where other normal functions can't be used - in pattern matching. So these need to be distinguished from the normal function declarations in the environment.

        Typechecking the datatypes involved making their constructors into suitable constants or functions and then adding them to the environment in a way that distinguishes them from other plain functions.

        The and facility was added to data types to allow datatype definitions that refer to each other.

        It is not possible to allow a type to be assumed for any part of the datatype declaration or to investigate the type of any part of the datatype declaration.

      4. Pattern matching

        5. To deal with typechecking, each individual pattern is treated as a function on its own and at the end they're all unified and the resulting type is given as the type of the whole function.

        In the case of pattern matching the way in which type errors are dealt with is that if any of the patterns have a unification error then none of the patterns in the function are unified. If all the patterns typecheck correctly, using clones of the patterns, an attempt is made to unify the whole function. If this fails then none of the patterns are unified with each other. If it succeeds then the type of the function is taken to be the result of unifying all the patterns.

        The reason for dealing with errors in this manner is that if the unification is to fail at this point then it fails because the patterns are inconsistent. So if the patterns are looked at individually before any unification takes place it might be clearer why unification has failed. Whereas if unification has been performed the reason for failure may not be obvious from the changes that were as a result of the unification.

      5. Derived expressions

        6. The while, fun and case constructs were added to the language. There was no need to modify the typechecker to deal with the fun and case constructs as these could be rewritten in terms of existing constructs.

        In the case of while, it seemed too complicated to put it back to its original form so the typechecker was modified to deal with this separately using the inference rule

      6. Exceptions

        7. The addition of exceptions was limited in that they are not allowed to carry polymorphic values. The typechecking algorithm was extended using the following inference rules

        The declaration of exceptions was dealt with in a similar manner to the way in which datatypes were added. The declaration was turned into a constant or a function and added to the environment. So for example exception e of int would add a function int® exn to the environment.

      7. Eqtypes

        8. Equality types were added to the typechecker. This meant that the operator

        equals : ''a * ''a ® ''a

        was available. While the addition of equality types is relatively straightforward when the set of data types available is fixed, the addition of user-defined datatypes required extra work. When typechecking for the first time it was decided to determine which datatypes admit equality. Also the construct and is allowed for datatypes. As the datatypes can refer to each other, discovering which datatypes admit equality was tricky.

      8. Overloaded Operators

The overloaded operators plus and minus were added to the initial environment. They are allowed to be overloaded with int or real type.

  1. Goal 1: Find type of expression

    2. This chapter describes the method used to realise the first project goal i.e. finding the type for an expression.

    1. Identifying the type

      2. As described earlier the parser builds a tree representation of the program. The typechecking process then populates the tree with the appropriate type / error information. This means that, after typechecking, the type of any node is immediately available without the need to do any extra work with the code.

      So instead of the problem being to identify the type of a node it is now to identify which node to read the type from.

    2. Identifying the expression

Any expression in the original code can be chosen. This may be a complete expression or a partial expression. As a result it may span several nodes in the tree. There are a number of possible ways in which the nodes relevant for an expression could be identified:

  1. Re-parsing

    2. The expression could be parsed again to build a node structure. The tree representation of the original program could then be searched for the required nodes.

    This approach would only be feasible if a complete expression was being located. If a partial expression was selected then the parser might not have enough of the original expression to parse it correctly. For this reason this possible approach was discarded.

  2. Recording extra information when first parsing

An alternative approach is to store extra information for each node when the parsing is first being carried out. As each node is created the region of the source code that results in the expression is stored with it.

With this information available it is possible to scan the program tree to find all nodes that overlap the selected expression or part expression.

This is the approach that has been chosen.

A number of nodes will have been identified as being related to the selected expression. The return type may or may not come from one of these nodes. The only sensible process that can be used to obtain the return type is to identify the lower level node in the tree that completely encompasses the selected node(s) i.e. the higher level expression that contains the selected expression parts.

For example,

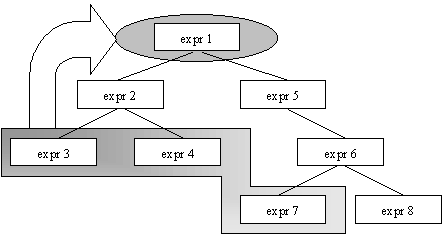
If the nodes containing expr 3, expr 4 and expr 7 were identified as being part of the required expression then the lowest level encompassing node is the one containing expr 1.

    1. Example

Consider the following example:

fn (x, y, z) Þ if x then
cons (x, cons(y, nil) )
else
cons (y, x)

This will lead to the following tree:

 

 

 

 

  1. To find the type of the expression cons(y, nil) the nodes marked as region 1 will be identified. The result will then be taken from the cons node and the resulting type will be b list.

    2.  

  2. To find the type of the following partial expression, the nodes from region 2 will be identified.

fn (x, y, z) Þ if x then
cons (x, cons(y, nil) )
else
cons (y, x)

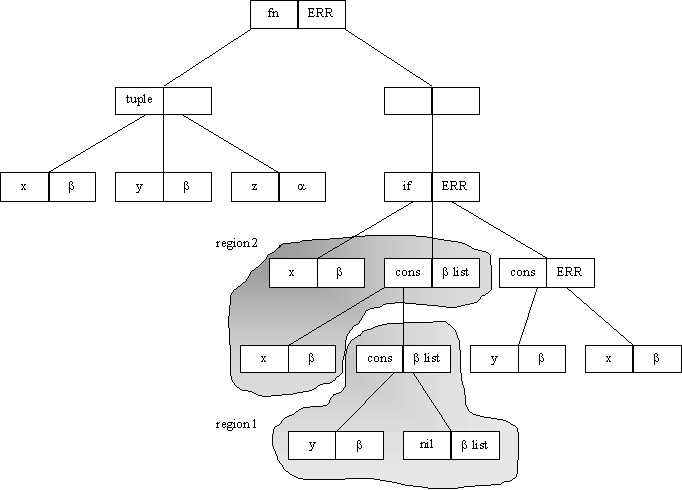
To find the actual type the lowest level enclosing node is required. In this example this is the node with the if. So the resultant type will be an error.

  1. Goal 2: Assume type for expression; first approach

    2. This chapter describes the first attempt that was made in implementing this goal.

    1. Localised re-typechecking

In trying to change the type of an expression, the first attempt that was made involved trying to perform the minimal amount of typechecking possible. This involved just re-typechecking any expression that contained a change and using the types that had already been generated for the other unchanged expressions. In effect what's happening in terms of the tree, is that is a change is made a particular node, then this node and the nodes above it (that contain it) are changed. The remaining nodes will remain unchanged.

Consider the following example:

if (expression1) then
(if (expression11) then
expression12
else
expression13)
else
(expression2)

If a change occurred in expresson12 then the types of the following terms would have been unified again:

  1. expression12 with expression13

  2. expression11 with bool (as it is contained in the same expression as expresssion12 and expression 13)

  3. expression2 with the result of the unification in 1

  4. expression1 with bool

Note that for expression1, expression11, expression 13, and expression2 no typechecking would have been performed on any part of them. The type used would have been the type that was originally stored on the tree.

    1. Advantages

      2. The approach was the most obvious one that came to mind. It had the advantage that the whole expression would not have to be typechecked and so it should represent a reasonably efficient implementation.

      Secondly it seems straightforward and logical and was easy to implement.

    2. Problems

However several flaws emerged with this approach.

Consider the case of

let f = . . . in . . f . .

If for example a change is made inside the declaration of f , then the definition of f in the declaration part of the let should get the correct type. However in the body of the let, the type used for any instance of f will be the old type and not the new type that has resulted from the change. (This is as it is not above the level of the change on the parse tree and only changes that are directly above the expression being changed will be modified). Because of this making a change to the f in the declaration is not very useful as the f in the body won't be affected.

The other main problem that existed is that each time a change is made it is necessary for the types of the parameters to be reset. Consider the following example

fn (x,y) Þ if x then y else 1

If the type of the 1 in the else branch was overridden with type string and y parameter hadn't been reset (i.e. y still has type int) then this valid change would result in a type error. However if the y parameter is reset, then everywhere else that the y occurs needs to be updated and typechecked. The difficulty is that these occurrences of y may be outside the area in which typechecking is being done and so they will not be updated and typechecked.

This approach was the first one considered but upon investigation revealed itself to represent an incomplete solution. An alternative approach had to be developed, which is described in the next chapter.

  1. Goal2 : Assume type for expression; second approach

    2. From trying the approach outlined in the previous chapter, it became obvious that the entire expression would need to be re-typechecked. This chapter describes the approach that was settled upon to achieve the second goal of assuming types for expressions. In essence it involves fixing the types at particular nodes and re-typechecking the complete expression, taking care to exclude the nodes that have been fixed (and any nodes beneath them).

    1. Possible strategies

      2. There are two possible strategies that can be used when the expression is being re-typechecked.

      1. Re-typechecking from the beginning

It would be possible to take the expression and re-parse it. The new tree generated could then be typechecked again in conjunction with a record of the changes that need to be made.

However, while dealing with changing the type of an expression in this manner is quite straightforward, several points need to be considered.

The first two points bulleted above are not significant problems as the expressions that are dealt with are small for the most part. However if the expressions become large then this method could be inefficient.

      1. Using the tree already present

The other strategy would be to try and use the data structure that has already been created.

The benefits of using the existing tree are

The strategy settled on was to use the existing tree, as it made the implementation of making a sequence of changes and assuming polymorphic types slightly easier. This strategy is more efficient than creating a new tree every time a change is made.

    1. Overview of the approach

      2. The approach taken is to re-typecheck the tree that already exists. The same principles described in Chapter 4 regarding error handling are followed when re-typechecking an expression to make a change. i.e. the re-typechecking continues after an error is encountered to try and collect as much information as possible.

      The relevant information from the initial environment that was needed to typecheck the expression was stored on the tree the first time that an expression was typechecked. This meant that when changes are being made to the expression all the information necessary to re-typecheck the expression is present on the tree. e.g. cons is present in the initial environment before any typechecking takes place. Any time that cons is used during the initial typechecking, its value is stored on the node on the tree. This then allows a copy to be made of it during the re-typechecking process so the initial environment is not needed.

      Once the typechecking process started it was necessary to create an environment to store the relevant type information regarding all the variables introduced in the expression. This meant that when these variables were changed, their changed types were added to the environment. As a result of the new changed types being in the environment, anywhere that these variables were used the new changed types were used.

       

    2. Implementation decisions

      3. The following are some of the implementation decisions.

      1. Recording the results of changes

        2. When a type is assumed for an expression and the re-typechecking carried out, the types of other expressions can change. It was decided to store these new types on the tree, as this would allow the results of the change to be investigated. If they were not stored and a further error occurred then there would be no way of investigating the additional error.

        During the initial typechecking a copy of the tree is generated. This means that the copy can be used to make changes to and the original can remain untouched and is available at all times for comparison purposes.

      2. Inside an assumed expression

        3. When the type of an expression is being given an assumed types, what happens inside that expression ?

        If X is an expression that has a type assumed for it. No typechecking can take place inside of X, however for consistency purposes it was decided to make the types of an identifiers inside of X consistent with the types that the identifiers have outside of the expression X. (This is useful for implementing the focussing feature described later.)

        The process described above can be illustrated using this example,

        fn (x, y) Þ cons(x, cons(y, x))

        This will result in a type error. The type of y is currently 'a. If the type of cons(y, x) is fixed at int list, the whole expression will now have type

        int * ‘c ® int list

        The typechecking algorithm has been modified to ensure that the types of identifiers are consistent throughout the whole expression. This results in the type of y inside the cons(y, x) having type ‘c. If the changes were not made the y inside the cons(y,x) would still have type 'a.

        However inside an assumption no unification will take place at all as this may adversely change the types outside of the expression.

      3. Conflicting assumptions

        4. What happens if a type is assumed for an expression that already has a type assumed for it or part thereof ?

        If a type is assumed at a node that had a type previously assumed for it, then this new type assumption will replace the old type assumption

        If a type is assumed for a node, and some node below it has an assumed type then they both remain and the assumed type of the higher placed node will be used.

      4. Effect on terms within expression

      When the type is assumed does it imply anything about the expression that it deals with ?

      When a type is assumed for an expression, it does not imply anything about the term. No attempt is made to unify the type of the expression with its type assumption.

    3. Features

      4. The following are some of the features of the implementation.

      1. Let-bound variables

        2. The problem encountered with let-bound variables in the last chapter, whereby the occurrences of let-bound variables weren't updated no longer applies now that the whole expression is being re-typechecked. As a change is made to the let-bound variable, it is added to the environment and as a result modified everywhere that it should be.

        Consider the example,

        let fun id ( x ) = x in

        fn x Þ if id (true) then id (x) else x

        The type of this expression will be

        ‘a ® ‘a

        If, for example, the x in the body of the id function is changed to have type bool then the type of the whole expression will now evaluate to

        bool ® bool

        What's happening is that when the type of the id function was changed, it was added to the environment with the new type. Anywhere that the id function is now called it uses the type currently in the environment, which is bool ® bool.

      2. Lambda bound variables inside of a function

When dealing with assuming types for parameters, there are two different cases

Consider a function of the form

fn ( x , y ) Þ if true then x else y

This expression will have type ('a * 'a ® 'a).

If a type of int is assumed for the x in the parameter part of the above function then the entire function now typechecks to have type int * int ® int . The x was changed in the body and so the parameter y ended up with an int type as a result of being unified with the x in the body.

However if instead the x in the then part of the conditional had been changed to have type int then the expression would have typechecked to have type ('a * int ) ® int. The reason that the y is changed to int is as a result of unification in the if then else . However the x in the parameters remained unchanged.

      1. Sequence of changes

Each time that a change is made, details of the change are stored on the appropriate node. When a further change is made to the tree, it is re-typechecked and when a node with an assumed type is encountered this assumed type is returned as the type of that node.

    1. Focussing in on error terms

      2. A natural way of trying to identify and fix an error, is to first identify the general expression that the error occurs in. When this is found then an attempt is made to try and find a smaller expression inside of it that contains the error, and you keep going like this to try and hone in on the error.

      Focussing in should allow the user to assume a type for an expression and if this change allows the whole expression to typecheck, then they can try and fix up the inside of this expression to what it should be. So most of the functionality needed to provide a focussing in facility should already be present as a result of the two goals of the project.

      1. Solution

        2. It was decided to use the same tree that is used to try out type assumptions. This ensures that the relevant information from outside the focussed expression that is needed is available.

        When an expression is focussed in on, it is a matter of typechecking the sub-tree that represents the expression being examined. As one of the design decisions described in section 7.3.2 was to allow the types of identifiers changed outside an assumed type to be updated inside the assumed type, all the appropriate types needed are stored inside this sub-tree. To focus in and find the type, it is merely a matter of typechecking this sub-tree on its own.

        When the user is finished focussing in on a term, it is simply a matter of re-typechecking the whole tree to set it back to its original state.

        Repeated focussing in, just involves making sure that the relevant terms are typechecked separately in the correct order.

      2. Finding the types of expressions inside a focus

        3. To allow the types of various expressions to be found it is just a matter of returning the type at the appropriate node. See Chapter 5.

      3. Changing the types of expressions inside a focus

A slight problem exists when making a change inside of a focus. Consider the case of

let fun ex x = if true then x else "da" in pred(ex(1))

if the if true then x else "da" is being focussed on then the x will have been set to string and if an attempt is made to assume a type of int for the "da" expression then an error will occur. So it is necessary to allow the x to be refreshed each time a change is made.

To allow for this problem, when a change is made inside the focus, the whole tree is typechecked to allow the variables to be reset. (Any identifiers inside an assumption/focus will get the correct type, however no other typechecking will be performed inside a focus/assumed type - section 7.3.2). Then the focussed expression is typechecked in conjunction with the new change to be made.

The reason that the typechecking is performed separately for the focus term and not all at once is to avoid the following situation.

let fun ex (x) if x then ex(not(x)) else 1 in pred(ex(1))

A type error results from trying to apply ex to 1 as it's expecting an argument with bool type. So if the type int is assumed for if x then ex(not(x)) else 1 , this whole expression will typecheck correctly now.

Suppose the if x then ex(not(x)) else 1 term is focussed in on and the 1 is changed to string. If the whole term was now typechecked including the focussed term then an incorrect type would be assigned to the ex function (as a result of the focussed term being typechecked at the same time). So inside the focussed expression the type used for the ex function would be the old type. This could be a possible source of confusion for the user as they may think it should have the type that it had previously as a direct result of the change made.

This is the reason that when a change is made the whole expression is typechecked and nothing under the assumption is typechecked (except for the types of identifiers being updated). Then the focussed term is typechecked on its own.

 

To provide the functionality to allow for a focussing facility did not require a great deal of extra work as it involved modifying what already existed.

 

  1. Goal 2: Assuming polymorphic types

    2. When a assuming a type that contain only type operators, e.g. int , bool ® string, there is no problem with interpreting what the type int or bool means. However if the type contains a type variable then a problem can arise.

    1. The problem

      2. When the type to be assumed contains a type variable from some part of the expression then what does it mean ? If all the type variables remained constant in the process of assuming a new type, then there would be no problem. However new type variables are being introduced each time a change is made. So when an assumption contains a reference to ‘a, and it comes around to using this assumption, ‘a may no longer refer to a type variable that's currently used in the expression.

      To illustrate the point consider the following example,

      fn (x , l, y) Þ if x then cons(x, x) else cons(x, l)

      This will result in the following tree:

      This will fail to typecheck as a result of the cons (x, x). The requirement may be that the type of the second x in cons (x ,x) should be given the assumed type 'c list, where the 'c is meant to represent the type of the parameter y. However if the x is given the type 'c list, when the whole expression is typechecked again, the x, l and y in the parameters will be given new types initially, shown below. These will later change as a result of typechecking the body of the function.

       

       

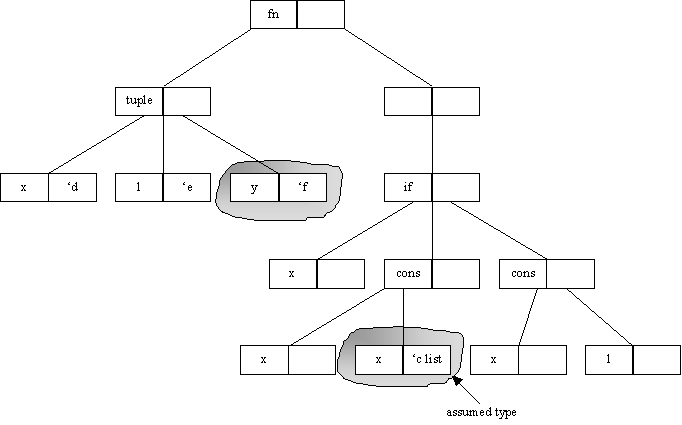
      As a result of the parameters being given fresh type, the 'c list won't actually refer to the y because ‘c is no longer the type of y. In this case it will typecheck successfully, but will typecheck to

      bool * bool list * 'f ® bool list.

      If the constraint had been used as it was intended the result should have been

      bool * bool list * bool ® bool list.

    2. The solution

      3. To solve this problem the concept of a truetype has been introduced. All parameters in a function definition will be assigned a truetype. A truetype once assigned will not be changed and can be used to uniquely identify a parameter.

       

      In the case of the above example a truetype of ‘A would be assigned to x, ‘B to l and ‘C to y as shown below.

       

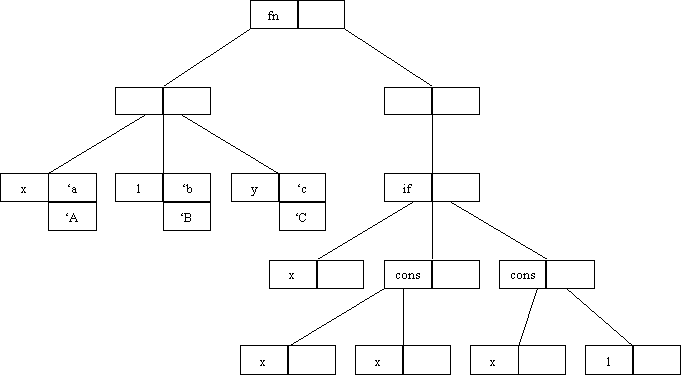
      When typechecking first occurs a new table will be used to store the relationship between truetypes and their current instance.

       

      TrueType

      Current instance

      ‘A

      ‘a

      ‘B

      ‘b

      ‘C

      ‘c

       

      When a type is assumed for an expression this table will be checked to see if the assumed type contains any of the truetypes present in the mapping table. If an entry is found then the assumed type is altered by replacing each current instance with its true type. For example using the above table,

      ‘a * ‘b ® int * ‘a

      becomes

      ‘A * ‘B ‘® int * ‘A

       

      Reconsider the previous example. Once again, assume a type of ‘c-list for the second x parameter.

       

       

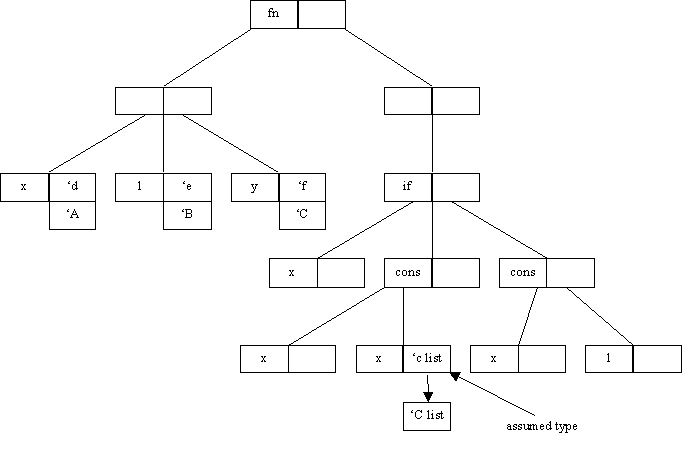
      The table is searched and the entry for ‘C – ‘c is found. This allows the assumed type of ‘c list to be changed to ‘C list.

      When the typechecking occurs again the table will have been updated to hold the new instances, as shown in the table below,

      TrueType

      Current instance

      ‘A

      ‘d

      ‘B

      ‘e

      ‘C

      ‘f

       

      When the assumed type ‘C list is encountered during the typechecking process, the table is searched for ‘C. When the record ‘C – ‘f is encountered the type for that node that will be returned is ‘f list. The ‘C will remain stored on the tree to ensure the types will remain consistent through further changes.

      1. The steps

The process described above can be summarised by the following steps:

  1. Initially when a parameter is added to the environment a true type is generated and stored for that type. If a parameter is itself a datatype constructor then truetypes are assigned to its parameters instead.

    2. For example, fn(cons(x, l), y) will result in truetypes for x, l and y – not for cons(x, l) and y.

  2. When an assumed type is being added, the table will be used to change any of the current instances included in the assumed type into a truetype. The assumed type will now contain the truetype and this is what is stored on the tree.

  3. When typechecking occurs again, the table is updated to hold the new instances for the truetypes.

  4. When an assumed type is encountered the table is searched to change any truetypes in the assumed type into current instances.

    1. Example

      2. Consider the following example,

      let fun id (x) = 1 in

      fn (x,y,nil) Þ (id(x), id(y) , nil) |

      (x,y,cons(z,l)) Þ (id (x) , id(y) , z)

      This expression will typecheck to have type

      ( ( 'a * 'b ) * 'c list list ) ® ( ( int * int ) * 'c list )

      However, the id function has been declared incorrectly. In this case the type of the id function should be of the form 'A ® 'A. If a type is to be assumed for the body of the id function, it needs to be the same type as the type of the parameter x. (If any other polymorphic type was assumed other than the type of x, then the dependency between the parameter and the body would be lost.)

      In this case the true type of the x is 'd, if the type of the body of the id function is now set to 'd then the resulting type is

      ( ( 'e * 'f ) * 'g list list )® ( ( 'e * 'f ) * 'g list )

      While the names of the polymorphic types will not remain the same, the dependencies are shown. i.e. the type of x is of type 'e and the type of id(x) is also of type 'e. The same holds for the y parameter.

      Now the other problem that needs to be fixed is that the type of the cons (x,l) should just be a list, not a list of lists. For z in the very last part of the function, the type that needs to be assumed is a list of elements of same type as z. There are several ways of doing this,

      The type of cons in the parameters is ('h * 'h list) ® 'h list

      The type of the z is 'l.

      The type of the l is 'j.

      Any of the following can all be used to assume the type required

      'h list

      'l list

      'j (this is because this has not yet been set to a list)

      By assuming any of the above types, it will result in the following type,

      ( ( 'k * 'l) * 'm list )® ( ( 'k * 'l) * 'm list )

      Again the result of the type of the result of the function is consistent with the arguments. The other point to note is that these changes have been made on top of each other . So the change involving the id function has remained and is unaffected by further changes.

    2. User supplied polymorphic types

      1. The problem

In the case of the user defining their own types, the following problem exists,

When a type is assumed containing a type variable unknown to the typechecker, there needs to be some way of resetting the value back to a fresh type variable each time a type is assumed. For example in ,

fn (x,y) Þ if x then y else 2

if the y is given a new polymorphic type say 'A, then it will be instantiated to int during the typechecking. If however the type of the 2 in the else branch is then changed to have type string., then as the assumed type of y is now of type int, a type error will occur in trying to unify the type int and string. So it is necessary for the assumed type of the y to be reset to type 'A before any more changes are made to the expression.

The other point that should be noted is that when something is set to have type 'A then if in a further change, 'A is referred to again, what is it actually referring to ? There are two possible options

  1. Each time the 'A is referred to (in further changes), it is referring to totally different types.

  2. In the course of changing an expression, every time the 'A is referred to it refers to the same type

The preferred option in this case would be the second. This would mean that a user defined polymorphic type can be used in several places.

These problems are similar to the ones encountered in trying to allow the user to assume the types of polymorphic variables used in the expression as described above in Section 8.1. So the solution to it should be very similar to the one already described above.

      1. Solution

        2. When a new type variable is introduced by the user, it is added to the truetype mapping table. The new type variable is treated like a truetype.

        This truetype is then stored as the assumed type on the node. Any time that it is used, the table is searched to return its current instance.

        This means that the problems discussed above can be dealt with in a satisfactory manner and that user defined polymorphic types will remain consistent through a series of changes.

      2. Example

To show how the types remain consistent through a sequence of changes consider the following example,

fn (x,y) Þ if x then 1 else x

Initially this will fail to typecheck. If the x in the else part is changed to type 'A, then the whole expression will now have type

bool * 'c ® int.

 

 

However if the type of the argument y is now given a type 'A, then the function will now have the type

bool * int ® int.

So the 'A is recognised as being the same type as the x parameter and as this is currently set to int, the type of y will now become an int.

If the 'A hadn't been recognised as being the same type assigned to the x in the else part previously, then the resulting type from typechecking it would have been

bool * 'd ® int

 

So a solution has been provided that allows the user to define their own types and for these types to remain consistent across a sequence of changes to an expression.

  1. User Interface

    1. Requirements

      2. One of the underlying goals of this project was that whatever tools were developed should be easy to use and should be quick to use. In essence they should provide a ‘point & click’ approach to type debugging/checking. For example, instead of re-entering an expression to examine its type a user should be able to point at or mark the expression on the screen and click a button to obtain the type information.

    2. Java

Java was chosen as the implementation language for the project. This decision was made for a number of reasons:

    2. The main window

The following window was designed for the purposes of this project:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

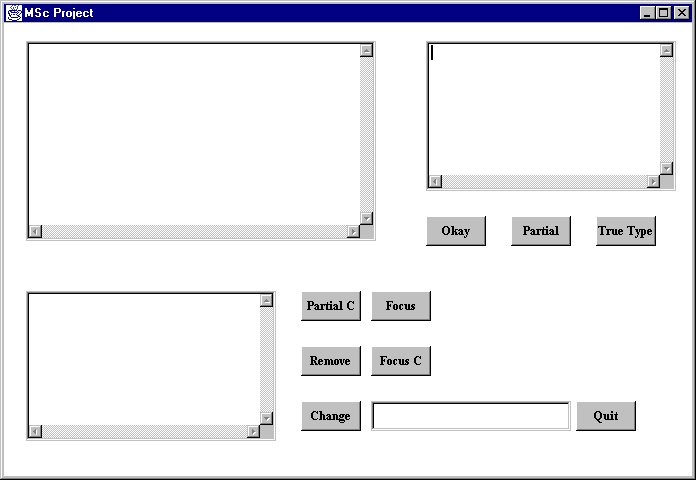
There are four parts to the window:

  1. the top left hand section contains the code that is being typechecked

  2. the top right hand section is used to provide feed back to the user about the type information of expressions and the result of the typechecking.

  3. the bottom left hand section provides a secondary feed back window and is used when types are assumed for expressions. A secondary window is used so that the initial type information can remain visible in the primary output window.

  4. the remaining areas contains the buttons that are used to perform the various functions that are available and an area for entering the type expressions.

 

 

The following buttons are included:

The next chapter provides a complete example of how this interface can be used to debug and correct type errors.

  1. Case study example

    2. The example used is shown below.

    Step 1

     

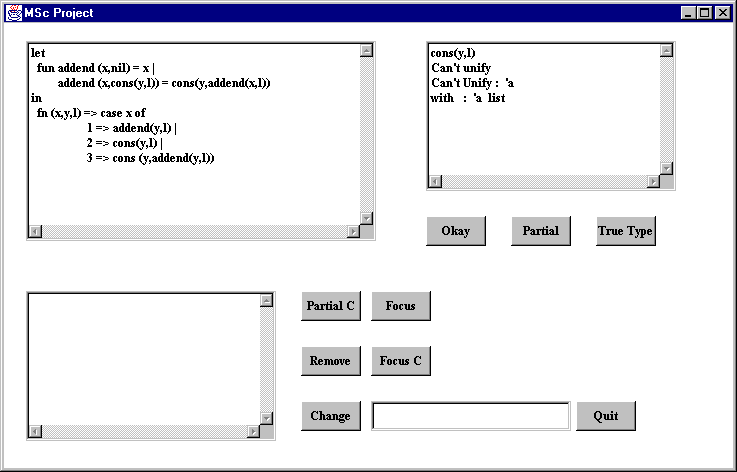
    The problem with this particular example is that an error was made when entering the function addend. The addend is supposed to add an element to the end of a list. In the first pattern, the x to the right of the = should read as cons (x, nil). This, however, is not what's causing the error. The error is occurring when the user is applying the function thinking it has the correct type.

    The first time that the expression is entered and typechecked, the resulting window is shown. The resulting error is displayed in the top right window. The cons(y,l) means that the error occurred somewhere in the cons(y,l) expression.

     

     

     

     

     

     

     

     

     

     

     

     

    Step 2

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    Step 3

     

    There are several ways of trying to discover the cause of the error. Here it was decided to give a dummy type to the erroneous term to see if this will allow the term to typecheck. This was done by introducing a new type 'dummy and assigning it to the expression selected (cons(y,l) ).

    However a further error has been highlighted in the next branch of the case. Details of the error are contained in the bottom left window below.

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

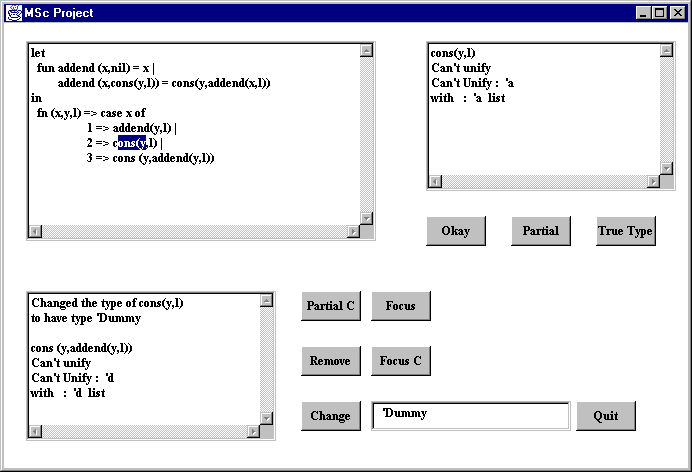
    Step 4

     

    The same approach used in Step 3 was taken in dealing the with error here. i.e. another new type variable was assumed for the erroneous term. This allowed the whole expression to typecheck and the resulting type is shown in the bottom left window below. However the type shown is not the type expected, the y parameter has type 'e list and there is no reason for it to be a list.

     

     

     

     

     

     

     

     

     

     

     

     

     

     

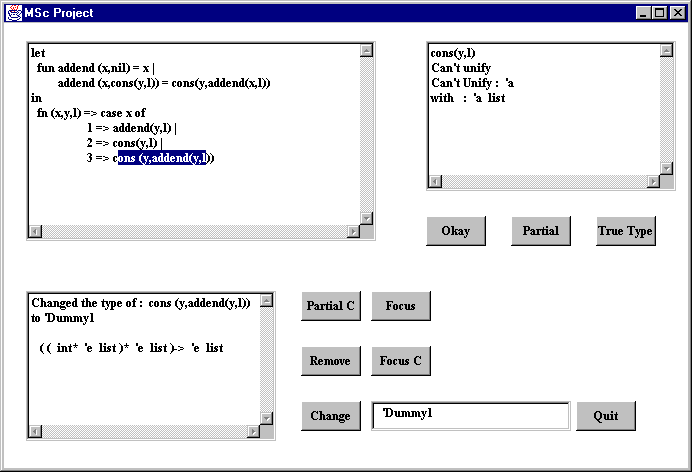
    Step 5

     

     

     

     

     

     

     

     

     

     

     

    Step 6

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    Step 7

     

    To change the type of the x in the body, it is necessary to get the truetype of the x. (If a new fresh type was assigned to the x in the parameter, then the resulting function type would not have the dependencies that should exist between the parameters i.e. addend would get a type of 'A * 'B list ® 'B list). So the true type of x is found and this true type is still displayed in the top right window. Then the type of the expression x in the body is changed to have type 'g list. This allows the whole expression to typecheck. Furthermore, the parameter of y in the main function is no longer a list.

    Previously when the expression typechecked in Step 4 it had the wrong type,

    int * 'e list * 'e list ® 'e list

    Now it has the type expected.

     

     

     

     

     

     

     

     

     

     

     

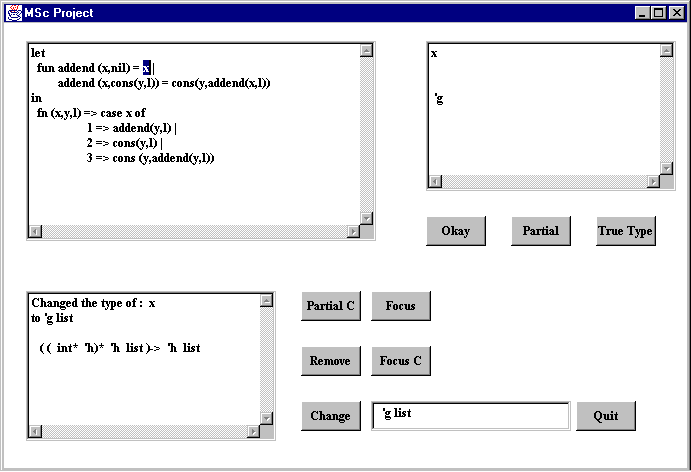
    Step 8

     

     

     

     

     

     

     

     

     

     

     

    Step 9

     

     

     

     

     

     

     

     

     

     

     

     

    The approach taken in the case study example was to effectively block out the expressions containing the type errors to allow the type of the error to be pinpointed. When the true error was thought to have been fixed, the other constraints were removed to ensure that the error had indeed been identified and fixed correctly.

    A number of other approaches could have been taken. For example when the value of y in step 2 was shown to be of type list, then the other expressions could have been investigated to discover the reason for this type. In this case it might have meant that the mistake in the addend could have been picked up more quickly.

    This example illustrates that the user has control over the manner in which they wish debug type errors.

     

  2. Summary and conclusions

    1. Realisation of goals

      2. The two project goals (to be able to show the type of an expression and to be able to change the type of an expression) were completed successfully for a small ML like language.

      The first goal proved to be reasonably straightforward when the correct data structures were used.

      The seconds goal turned out to be considerably more difficult and involved a level of complexity that was not initially evident.

      The point & click interface was completed that makes the selection of expression quick and easy.

    2. Extensions

      1. Extending for ML

        2. The scope of the project was limited to a small subset of ML. A possible extension would be to try and extend the language used to cover the ML core language.

      2. ML kit compiler

        3. Even though the typechecker was based on the typechecker in [Car87] a significant amount of time was spent on implementing it. Another place where time was lost was on the construction of the parser. Every time that the language was extended it entailed extending the parser and then extending the typechecker.

        If this project was to be done again, it would probably be worthwhile to investigate further whether or not to use the ML kit compiler. If the ML kit compiler was used as a starting point then would that mean that time wouldn't have to have expended trying to get a working parser and typechecker. The other benefit with this is that it would be fully linked into a real ML compiler and would be of a more practical use to ML users.

      3. Improved error messages

        4. The error messages in this project could be improved upon. At present they only inform the user of the types that failed to unify, however this may been during the process of unifying two large type expressions. So in this case it would be useful to have been given information about the whole type expressions not just the two types that failed to unify.

      4. User interface

Sufficient time was not available to complete the user interface. They following extensions would make the interface easier to use and improve its effectiveness for debugging type errors:

 

This project was implemented in Java on a Microsoft Windows PC. When running it on the Solaris workstation some inconsistencies were noted. e.g. selecting terms on the screen with the mouse behaved differently on the two machines, Java on the Solaris failed to position some buttons properly on the screen. In general Java on the PC behaved better that the Java on the Solaris.

    2. Conclusion

Type errors in ML can be difficult to debug, so the aim of this project was to provide a tool that would useful in trying to debug code containing type errors.

The tool that was produced in this project is easy to use (although the user interface could be improved) and can be used in whatever manner the user wants. For example if they want to look at the types of the various expressions to try and discover the error that way, then they can. If on the other hand they wish to block out parts of the code to try and identify the error that way, then they can do that either. This tool is flexible in that it can be used in whatever way the user wishes to use it. There is no set path that needs to be followed when trying to debug the type error. The debugging process is still very much under the control of the user.

What this tool can do is perform some of the tasks that the user would normally perform manually when trying to debug a type error. e.g. finding the types of parts of expressions. Not having to do this speeds up the whole debugging process for the user. So this tool would be a useful aid to have when a type error is being debugged.

Appendix A Language

Exp

::=

Constant |

Ident |

(exp) |

exp(exp) |

exp1 andalso exp2 |

exp1 orelse exp2 |

exp handle match |

raise exp |

fn match |

if exp1 then exp2 else exp3 |

while exp1 do exp2 |

case exp of match

 
       

match

::=

mrule á | match ñ

 

mrule

Pattern

::=

::=

Pattern Þ exp

Ident |

Constant |

(exp á ,expñ )

 

  

decl

 

 

::=

Datatype datbind |

Exception Ident of type |

dec1 á then dec2ñ |

rec decl |

Ident = exp|

let decl in exp |

fun Ident pattern = exp

á |Ident pattern = expñ

 

datbind

::=

TypeVarList Ident = Ident á of Type ñ

á | Ident á of Typeñ ñ á and datbindñ

 

TypeVar

::=

' á 'ñ identifier

  

TypeVarList

::=

TypeVar |

(TypeVar á ,TypeVarñ )

  

Type

 

 

 

::=

 

 

 

TypeVar |

Type * Type |

Type ® Type |

(Type á ,Typeñ )

 

`

 

Appendix B Inference Rules

The following inference rules come from [Car87] are the infernece rules for the small language described in section 3.2

[IDE]

 

 

[COND]

 

 

[ABS]

 

 

[COMB]

 

[LET]

 

[GEN]

 

[SPEC]

 

[BIND]

 

[THEN]

 

[REC]

 

 

 

Bibliography

[BRTT93]

Lars Birkedal, Nick Rothwell, Mads Tofte, David N. Turner. The ML Kit (version 1). Technical Report 93/14, Department of Computer Science, University of Copenhagen, 1993.

[BS95]

Karen L. Bernstein and Eugene W. Stark. Debugging type errors(full version). Technical report, State University of New York at Stony Brook, Computer Science Department, November 1995.

[Car87]

Luca Cardelli. Basic polymorphic typechecking . in Science of Computer Programming,147-172, 1987.

[DB96]

Dominic Duggan and Frederick Bent. Explaining type inference. Science of Computer Programming ,(27):37-83, 1996

[FH88]

A. Field and P. Harrison. Functional Programming. Prentice-Hall, 1988.

[Hay93]

D. Hay. An Interactive Type Checker for Standard ML CS4 Project, University of Edinburgh, 1993

[JM97]

Yang Jun and Greg Michaelson. A visualisation of polymorphic type checking. Department of Computing and Electrical Engineering, Heriot-Watt University.

[McA98b]

Bruce J. McAdam. On the unification of substitutions in type inference. Technical Report ECS-LFCS-98-384, Laboratory for Foundations of Computer Science, The University of Edinburgh, James Clerk Maxwell Building, The Kings Buildings, Mayfield Road, Edinburgh, UK, November 1997.

[Mil78]

R. Milner. A theory of type polymorphism in programming. In Journal of Computer and System Sciences, No. 17, 1978

[MTHM97]

R. Milner, M. Tofte, R. Harper and D. MacQueen. The definition of Standard ML (Revised). MIT, 1997

[MT90]

R. Milner, Mads Tofte. Commentary on Standard ML. MIT, 1990.

[Set89]

R. Sethi. Programming Languages Concepts and Constructs. Addison Wesley 1985.

[Wan86]

Mitchell Wand. Finding the source of type errors. In ACM Symposium on Principles of Programming Languages, number 13, pages 38-43. ACM, ACM Press, 1986.