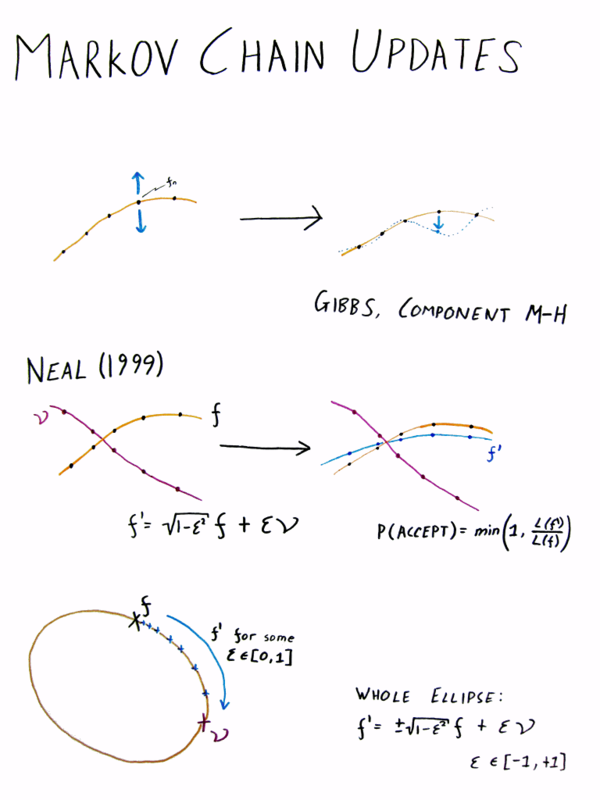
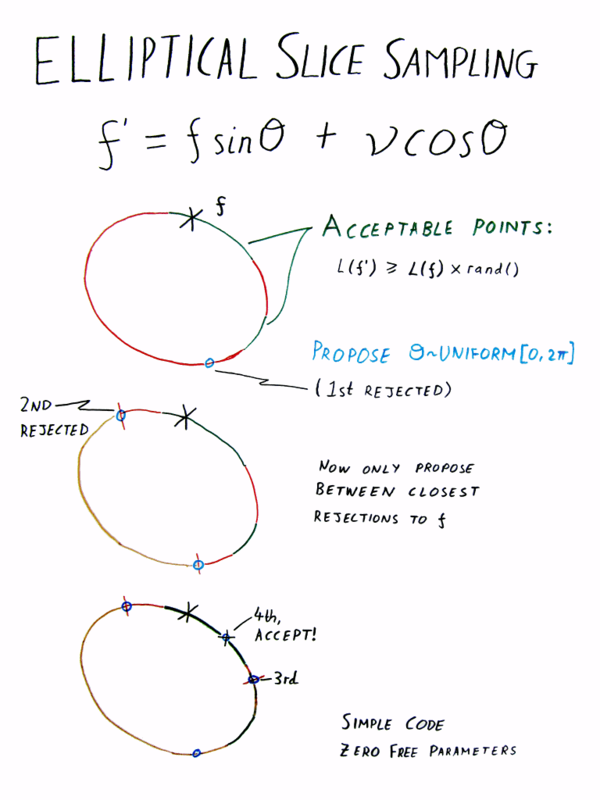
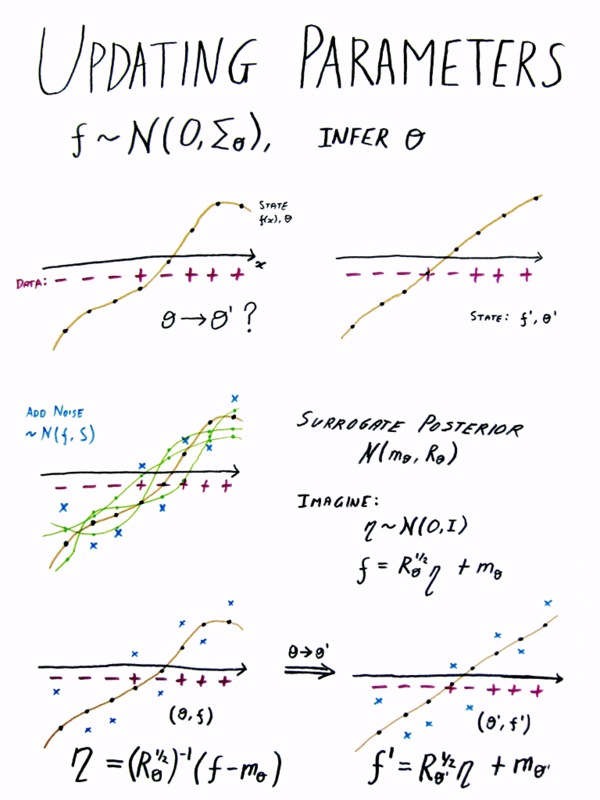
Elliptical slice sampling

This poster was presented at AISTATS 2010 as a visual aid while explaining Elliptical Slice Sampling. The fourth sheet was added for the Valencia Bayesian meeting 2010 to explain some of [arXiv/1006.0868].

A 1024 pixel high version for projecting in a journal club is available in poster.pdf.

Sheet 1. Setup: function with Gaussian process prior, with non-Gaussian likelihood. Task is to draw samples from posterior distribution over function values.

Sheet 2. Markov chain updates move function between plausible alternatives that explain data. Gibbs updates cannot move quickly as cannot keep function smooth if move one function value significantly without moving others at the same time. Neal (1999) suggested a clever update, which we use, but it requires setting a step size. This work considers all possible updates for different step sizes, which defines an ellipse of functions.

Sheet 3. Illustrates Neal's (2003) slice sampling algorithm, adapted to be run on an ellipse.

Sheet 4. We now consider Markov chain exploration of the plausible hyperparameters (also known as covariance or kernel parameters) for the Gaussian process model. We need a way to change the function to match the hyperparameters, or we won't be able to move the hyperparameters very far. The arxiv paper linked above provides a method.