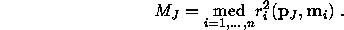Least Median Squares Estimation and Estimators
This page contains a description of the least median squares estimation
technique with a sample application. It also describes possible uses of
the technique in computer vision.
Introduction
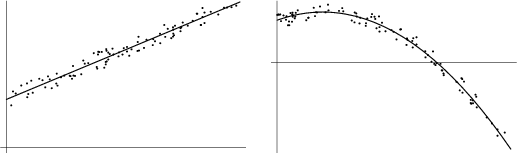
Least squares estimation is a technique used
to find paramaters for a given equation which is the best fit for a set
of data points. The idea is to minimise squares of the
offsets ("the residuals") of the points from the curve. The sum of the
squares of the offsets is used instead of the offset absolute values
because this allows the residuals to be treated as a continuous
differentiable quantity. However, because squares of the offsets are
used, outlying points can have a disproportionate effect on the fit, a
property which may or may not be desirable depending on the problem at
hand.
Least Mean squares tries to minimise the error over all of the
data points in the set. In the case of computer vision (due to digital
photography) the data in question is almost always noisy. This means
that there is a large number of outliers and least mean squares often
gives a poor fit to the data. One solution to this is to use least median squares estimation.
Least Median Squares Estimation
It is very difficult to define the whole algorithm for least median
squares as a mathamatical formula for a whole data set so an algorithm
that generates a least median of squares solution
for a data set is given below:
1. Pick m random sets of points with size p from the data set where p is the number of paramaters in the equation being solved.
2. for each subset use a method such as Least mean of squares to find a solution for the paramaters from that data set.
3.for each set of paramaters p obtained calculate the median of the squared residuals M with respect to the whole data set:
4. The solution is pj for which Mj is minimal among all mMj 's.
Least median of squares estimation is robust to outliers due to its
high breakdown value of 50%. This is the fraction of outliers that can
be tolerated whilst still returning a good solution. However the high
breakdown value means that LMedS does not cope well with Gaussian
noise.
Examples of Use
LMedS like many estimators can be applied
to problems in computer vision. Possible areas for use are fitting a
line to a set of points from an image, fitting a group of lines to a
set of points (such as a model), finding the optical flow in an image,
one area of particular interest is applying it to the discovery of the
Epipolar geometry of a pair of images to be used in stereo vision.
In this case the paramaters that the algorithm is estimating
are the rotation between the coordinate system of the two images, the
translation vector between the coordinate systems and the scale factor.
The data points that it is using are the pixel values from the image
that may be filtered in some way first.
The result of applying LMedS to the problem generates the following Epipolar Lines
Links
Equations from: http://www-sop.inria.fr/robotvis/personnel/zzhang/Publis/Tutorial-Estim/node25.html
Images from: A Highly Robust Regressor And Its Application In Computer Vision, E.Izquierdo
Further Information: http://www-sop.inria.fr/robotvis/personnel/zzhang/Publis/Tutorial-Estim/node25.html
Further Information:Least median of squares: a suitable
objective function for stock assessment models?, Kyle W. Shertzer and
Michael H. Prager, Available At: Link