Horizon Detection

Adam Nickerson :: s0199600 :: AV Practical 2

The horizon detection algorithm attempts to autonomously locate the horizon in an image. If a horizon is present and has been correctly located, it can be used as an aid to autonomous scene interpretation or as an aid to image compression.

A vision-based system can directly measure an aircraft's orientation with respect to the ground. There are two degrees of freedom critical for stability - the bank angle 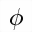and the pitch angle .
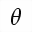The vision-based horizon detection algorithm lies at the core of a flight stability system and rests on two basic assumptions:

i) the horizon line will appear as a straight line (approximately) in the image, and
ii) the horizon line will separate the image into two regions that have a distinctly different appearance.
i.e. sky pixels will look more like other sky pixels, and less like ground pixels, and vice versa.

These basic assumptions can be transformed into a workable algorithm as follows: The first assumption reduces the space of all possible horizons to a two-dimensional (2D) search in line-parameter space. For each possible line in that 2D space, we must be able to tell how well that particular line agrees with the second assumption.
Therefore, the algorithm can be divided into two functional parts:

i) for any given hypothesized horizon line, the definition of an optimization criterion that measures agreement with the second assumption, and
ii) the means for conducting an efficient search through all possible horizons in 2D parameter space to maximise that optimisation criterion.

Colour, as defined in RGB space, has been chosen as the measure of appearance. This choice does not discount the potential benefit of other appearance measures, such as texture, but rather is a simple appearance model used as a starting point before moving on to more advanced feature extraction methods.

Assuming that the means of the actual sky and ground distributions are distinct (a requirement for a detectable horizon, even for people), the line that best separates the two regions should exhibit the lowest variance from the mean. If the hypothesized horizon line is incorrect, some ground pixels will be mistakenly grouped with sky pixels and vice versa. The incorrectly grouped pixels will lie farther from each mean, consequently increasing the variance of the two distributions. Moreover, the incorrectly grouped pixels will skew each mean vector slightly, contributing further to increased variance in the distributions.

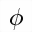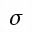Given the J optimization criterion derived in [1], which allows any given hypothesized horizon line to be evaluated, this horizon line which maximizes J must now be found. As stated previously, this boils down to a search in two-dimensional line parameter space, where the choice of parameters are the bank angle and pitch percentage (the percentage of the image below the horizon line) with ranges:

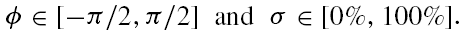
A two step approach in the search through line-parameter space is adopted, in order to meet real-time processing constraints. First, J is evaluated at discretized parameter values in the ranges specified above on down-sampled images with resolution 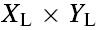. Then, we finetune the coarse parameter estimate from the previous step through a bisection-like search about the initial guess on a higher resolution image ().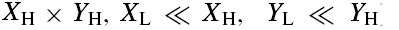

Thus, the horizon-detection algorithm can be summarised as follows. Given a video frame at resolution:

(i) Down-sample the image to 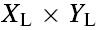, where .
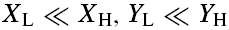(ii) Evaluate J on the down-sampled image for line parameters 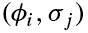, where:
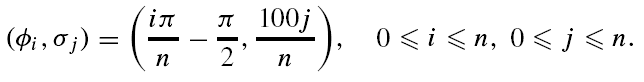
(iii) Select 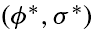, such that:
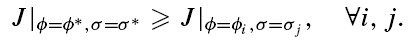
(iv) Use bisection search on the high-resolution image to fine-tune the values of

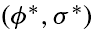
In aerospace, computer vision is used for a flight stability and control system, based on vision processing of video from a camera on-board micro air vehicles (MAVs). A vision-based horizon detection algorithm forms the basis of the flight stability system.

For instance, given that surveillance has been identified as one of their primary missions, MAVs must necessarily be equipped with on-board imaging sensors, such as camera or infrared arrays. Thus, computer vision techniques exploit already present sensors, rich in information content, to significantly extend the capabilities of MAVs, without increasing the MAV's required payload.

In geology, horizon detection is used in the analysis of rock formation and layer detection. When used for autonomous scene interpretation, a binary mask whose pixels indicate either sky or geology is returned. Knowledge of the location of the horizon can be used, in part, to measure the information content of an image and/or to autonomously reposition the camera so that more geology is captured in the image. For image compression, pixels above the horizon have been set to zero to facilitate a run-length encoding compression scheme. After downloading the image, the sky can usually be reconstructed to a visually pleasing degree from the pixel values in the thin band of sky that is intentionally left above the true horizon. (See images at bottom of page)

Source: [1]

Source: [2]

References:
[1] Vision-guided flight stability and control for micro air vehicles. Authors: Ettinger S.M.; Nechyba M.C.; Ifju P.G.; Waszak M. Source: Advanced Robotics, 1 November 2003, vol. 17, no. 7, pp. 617-640(24)
[2] Sky Detection Results (Marsokhod Field Test '99) http://web99.arc.nasa.gov/~vgulick/FieldTest99/sky_detector/sky.html