


Next: Specific Solutions of the
Up: The Fixed Viewpoint Constraint
Previous: Derivation of the Fixed
The first step in the solution of the fixed viewpoint constraint
equation is to solve it as a quadratic to yield an expression
for the surface slope:
|  |
(9) |
The next step is to substitute  and set
and set
 which yields:
which yields:
|  |
(10) |
Then, we substitute 2 r x = y2 + r2 - b2, which when
differentiated gives:
|  |
(11) |
and so we have:
|  |
(12) |
Rearranging this equation yields:
|  |
(13) |
Integrating both sides with respect to r results in:
|  |
(14) |
where C is the constant of integration.
Hence,
|  |
(15) |
where k = 2 eC > 0 is a constant. By back substituting,
rearranging, and simplifying we arrive at the two equations which comprise
the general solution of the fixed viewpoint constraint equation:
In the first of these two equations, the constant parameter k is
constrained by 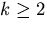 (rather than k>0) since 0 < k < 2 leads
to complex solutions.
(rather than k>0) since 0 < k < 2 leads
to complex solutions.



Next: Specific Solutions of the
Up: The Fixed Viewpoint Constraint
Previous: Derivation of the Fixed
Simon Baker
1/22/1998


