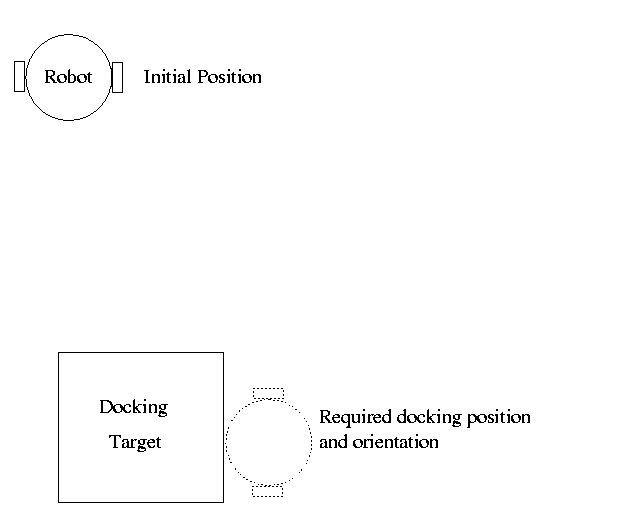
Docking is essential for a mobile robot that is required to perform precise interactions. Industrial fork-lifts, mobile manufacturing assembly robots, and rescue robots all need to move to an object of interest and dock with it to carry out their tasks.
Docking can be defined as moving from the current position to a desired position and orientation, while following a safe trajectory [2]. The final position and orientation of the robot must be adequate for the tolerances required by the particular task. A vision perspective definition is that a robot should move as near as possible to a target surface, without colliding with the target, and align its viewing direction with the normal to the surface [11]. In order to perform an operation on an object, such as manipulation or inspection, a robot generally needs to dock (e.g., a fork-lift robot docks with a pallet [6] to pick it up and move it elsewhere.) For a fork-lift robot: the object is stationary; position is in two dimensions (on the floor); and, orientation is rotation in one dimension (see Figure 1). For flying or underwater robots, position and orientation may each be defined in three dimensions (e.g., a helicopter landinge on top of a building.) However, the target point may also be mobile, such as capturing "free-flyers" using the "Mobile Servicing Station", which is a manipulator attached to the international space station [13]. In this case, the configuration still consists of a position and orientation relative to the target, but the target also has velocity relative to the environment.

Figure 1: A mobile robot in a starting configuration away from the target object, and the required position and orientation for docking.
In most cases, for docking it is essential that robot motion be controlled carefully while there is a danger of collision (i.e., the robot is close to the target). Particularly, in cases such as rescue submarines performing air-lock docking where contact is required. This differentiates docking from related problems of object interaction where the robot should apply an impulse, such as ball kicking in robot soccer contests.
In this section, we will treat the three sub-problems separately, while being primarily concerned with the second.
Moving close to object, can often be achieved using standard methods for navigation. The main task is to move to a location where the object will register adequately with the robot's sensors. See the CVonline section on Interactive Demo of Map-Building and Localisation in a Simulated Environment for an example of a general navigation mobile robotic system.
For high-precision docking, how close the robot must be before this sub-task begins is dependent on the size of the robot and object, but may be a matter of centimetres. High-precision docking is often performed using special purpose hardware, such as ultrasonics [1], or other range-finding devices. Mandel and Duffie [9] present a system that avoids the problem of high-precision docking for manipulation. They recognise features of a docking target surface and calculate the true relative pose. This is compared with the expected pose for which manipulator motions were calculated. Required manipulator motions can then be transformed based on this error.
Vision-based methods for approximate docking are common. Methods using other sensors such as sonar and laser range finders are also possible, but are not discussed here. Vision is an excellent sensor for the docking problem because high data rates can be achieved with low cost hardware. Further, vision allows systems to discriminate between objects with similar structure, which is difficult for range-sensor based systems.
Two distinct general approaches have been applied to the controlled-motion phase of docking: metric approaches, and active perceptual approaches.
These approaches estimate robot position in Cartesian coordinates, either world-centred or robot-centred. The robot plans a path and moves towards the goal on the basis of a series of one or more position estimates.
Arkin and Murphy [2] present a method for planning and executing such paths based on a potential fields [7] approach. The approach covers the first two phases of the docking problem. Ballistic motion is performed in an open loop manner with minimal sensory feedback. Ballistic motion is typically used for the first part of the docking problem, where the danger of collision is low. Controlled motion is performed in a closed-loop manner, where robot speed is dependent on the speed of perception. Controlled motion may include periods of inaction during planning. Typically, controlled motion is used in the second stage of docking where there is a danger of collision. Fitting into this approach, Vaughn and Arkin [15] present a recognition method that finds edges, and uses a Hough Transform (see the CVonline section on Hough Transforms), to identify the target object, and begin the controlled motion phase. Also, Lueth, Nassal and Rembold [8] present a robotic system for factory assembly, which uses global planning, and a combination of range sensors and vision to achieve docking.
Barnes and Liu [5] present a navigation system that performs the approximate docking operation as an application. The system recognises the target from an object model, calculates the inverse perspective transform to find the object's relative position, and then moves towards the docking surface. This system models the object from all angles that may be visible to the particular robot while travelling around it. The views are indexed by their order of appearance around the object, in a "canonical-view" model. This allows the system to approach from any angle, and move around the object to find the required docking surface. If the required surface is not visible, the robot moves perpendicular to the surface normal of the object to the required surface. The robot moves in for docking as soon it finds the required location, see Figure 2.
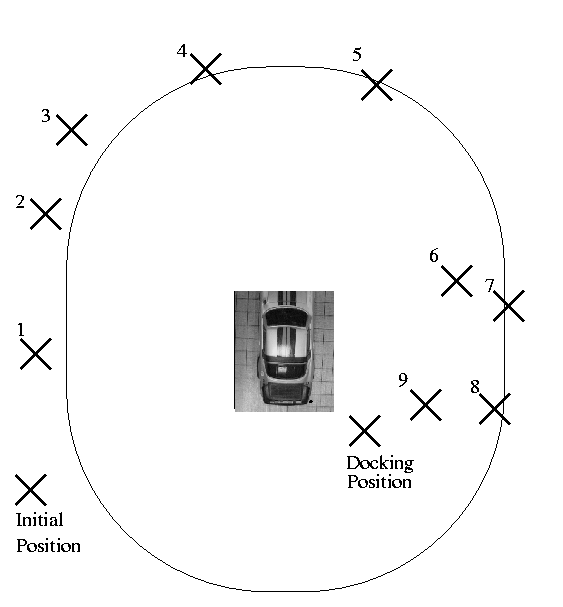
Figure 2: A path for moving around a model car and finally docking at the rear right-hand corner of the car.
Metric approaches can be easily combined with other path planning techniques that operate in world coordinates. Further, it is straight-forward to integrate additional spatial knowledge, such as connectivity between views of the target, or requirements for complex approach paths. However, metric approaches are often computationally expensive, and as a result have less frequent assessment of position, which can lead to drift away from the required path, or slow progress. Also, transforming from sensor coordinates to world coordinates leads to an additional source of numerical error.
A second approach is to discard the estimation of an external metric, and directly control the robot motion based on image parameters. The transformation to world coordinates is an overhead that may be unnecessary. Active perceptual approaches make use of fast vision methods that can be updated quickly so that the robot can converge to the correct position. If the measurements can be obtained at high speed, then the adjustment to motion based on any single measurement may be small. In this way, high precision in any given measurement becomes less important provided the robot converges toward the target location. This approach of controlling motion directly based on visual parameters is sometimes referred to as visual servoing.
Murphy and Arkin [2] present a region tracking method (see the CVonline section on motion) which forms the basis of a reactive docking procedure. If the required object is not centred in the image, the robot turns by at most three degrees, and repeats tracking until the object is centred. Once the object is centred, the robot moves approximately one foot towards it, and then continues tracking. In this case, and other examples presented below, there is no direct representation of metric world coordinates. Required actions are selected solely on the basis of visual parameters. This can be taken one step further, by controlling motors directly based on visual parameters. Also, the above method works based on kinematic measures; specifically distance and orientation to target. The methods discussed below operate based on equivalent measures in dynamic space, namely time-to-impact, and velocity perpendicular to the target.
Santos-Victor and Sandini [12] present an active perceptual approach to docking where all motor control is based directly on visual parameters in a closed loop. It is assumed that the docking surface is planar. The goal is to control the robot orientation in order to align the camera optical axis with the surface normal, and control the approach speed. The technique does not require three-dimensional reconstruction or calibration. Robot motion is derived directly from first-order space-time derivatives of the image, which provide fast robust estimation. Two aspects of robot platform motion are controlled separately: angular velocity (or heading direction); and, forward velocity. The control aim is to adjust heading direction so that the component of robot velocity perpendicular to the direction of the target goes to zero, i.e., the robot is heading directly towards the object. The forward-velocity aim is for the robot to move close to, but not collide with the target. The system uses two visual parameters derived directly from optical flow that measure perpendicular motion, and time-to-impact. The perpendicular motion measure is reduced to zero, and the time-to-impact (i.e., robot velocity over distance to object) is kept constant, so that when the object is infinitely close, velocity will be infinitely small.
Methods have also been derived for estimating time-to-impact using optical flow using log-polar cameras [14]. (A section on log-polar cameras will be added to CVonline soon.)
Barnes and Sandini [4],[3] present a log-polar variation on control of perpendicular motion. This is able to control the heading direction for general surfaces on the basis of assumptions about scene geometry that are plausible for a mobile robot. For example, given that the target is small in the image and the object is on the floor, all pixels below the object can be assumed to be closer to the robot than the object itself. Figure 3 shows a docking path generated by the method.
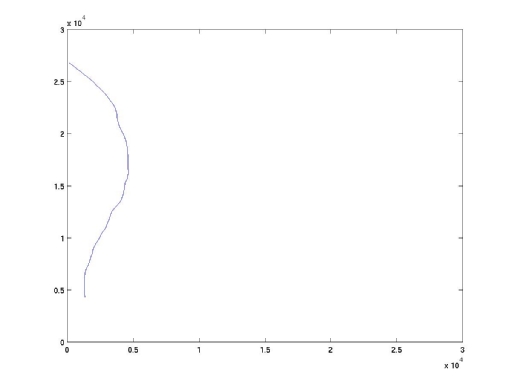
Figure 3: In a test performed in a simulator, the robot's initial heading was 45 degrees to the direction of the object. This plot shows the convergence of direction to be heading approximately towards the object. Control was based only on visual parameters. Note that the system cannot align with the surface normal as the object surface shape is unknown.
A key strength of the active approach is robustness. The approaches are all based on fixation or tracking of the target object, and centring it in the image. Further, as a deliberate consequence of methodology, active-perception methods obtain information from sensors frequently. These two facts make it less likely that the target object will be lost from the field of view. However, active-perception approaches for docking only perform a narrow range of functions. They generally rely on some other method to bootstrap by specifying the position of the target in the image. Also, the methods discussed above only move directly towards the goal. There is no in-built handling of obstacles, moving around the object if the goal surface is not visible, or adjusting to different orientations at the goal surface. Combination of active-perception based approaches with metric approaches is also possible (e.g., [1]), where the object is first recognised, and then handling is passed over to a tracking-based method for docking.
Last modified 7 November 2000