



Next: Minimization in One
Up: Theory: Optimization Methods
Previous: Theory: Optimization Methods
In the above we introduced functions of the form 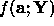 which measure
the fit of a model instance with n parameters a to some set of data Y.
We are interested in the optimal choice of parameters, those which give the
best fit to the data. This involves finding the optimum (maximum or minimum)
of the function
which measure
the fit of a model instance with n parameters a to some set of data Y.
We are interested in the optimal choice of parameters, those which give the
best fit to the data. This involves finding the optimum (maximum or minimum)
of the function 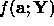 with respect to a. For notational simplicity
we will use
with respect to a. For notational simplicity
we will use 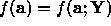 .
Since any maximum of
.
Since any maximum of 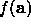 is a minimum of
is a minimum of
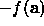 we will only consider minimization.
Formally
we will only consider minimization.
Formally 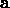 is a minimum point of
is a minimum point of 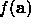 if there exists a region about a of radius
if there exists a region about a of radius  such that
such that
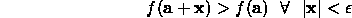
The maxima and minima of a function can either be global (the highest or
lowest value over the whole region of interest) or local (the highest
or lowest value over some small neighbourhood). We are usually most interested
in finding the global optimum (such as the model parameters which give the best
match to some image data), but this can be very difficult. Often a problem
will have many local optima (perhaps caused by image noise or clutter) which
means that locating the single global optima can be tricky.
The most suitable methods to locate minima depend upon the nature of the
function we are dealing with. There are two broad classes of algorithms.
- Local minimizers that, given a point in a `valley' of the function,
locate the lowest point on the valley.
- Global minimizers that range over a region of parameter space
attempting to find the bottom of the deepest valley.
If a good estimate of the position of the minimum exists we need only use
a local minimizer to improve it and find the optimum choice of parameters.
If no such estimate exists some global method must be used. The simplest
would be to generate a set of possible start points, locally optimize each
and choose the best. However, this may not be the most efficient approach.
Often an application will require both local and global methods. For instance,
in a tracking problem initializing a model on the first frame may require
a global search, but subsequent frames would only require a local search
about the current best estimate.
The choice of which local minimization technique to use will depend upon
- Whether a is one or many-dimensional,
- Whether
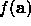 can be differentiated efficiently,
can be differentiated efficiently,
- How noisy
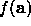 is.
is.
In the following we will give an overview of some of the methods for locating both global and local minima. For a more comprehensive survey, including algorithmic details, see [6].




Next: Minimization in One
Up: Theory: Optimization Methods
Previous: Theory: Optimization Methods
Bob Fisher
Fri Mar 28 14:12:50 GMT 1997
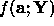 which measure
the fit of a model instance with n parameters a to some set of data Y.
We are interested in the optimal choice of parameters, those which give the
best fit to the data. This involves finding the optimum (maximum or minimum)
of the function
which measure
the fit of a model instance with n parameters a to some set of data Y.
We are interested in the optimal choice of parameters, those which give the
best fit to the data. This involves finding the optimum (maximum or minimum)
of the function 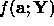 with respect to a. For notational simplicity
we will use
with respect to a. For notational simplicity
we will use 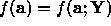 .
Since any maximum of
.
Since any maximum of 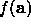 is a minimum of
is a minimum of
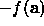 we will only consider minimization.
Formally
we will only consider minimization.
Formally 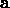 is a minimum point of
is a minimum point of 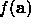 if there exists a region about a of radius
if there exists a region about a of radius  such that
such that




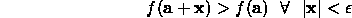
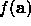 can be differentiated efficiently,
can be differentiated efficiently,
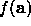 is.
is.