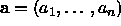Genetic Algorithms

Genetic Algorithms attempt to minimize functions using an approach analogous with evolution and natural selection. The key features are

• A point in the search space is encoded as a chromosome.
• A population of N chromosomes/search points is maintained, rather than just a single point.
• New points are generated by combining existing solutions.
• Optimal solutions are evolved by iteratively producing new generations of chromosomes in which good solutions are combined (bred) and bad ones discarded.

Usually a chromosome is a string of bits formed by concatenation of the bit strings representing each of the n parameters 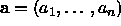. The number of bits used to encode each parameter will depend on the desired tolerance.

Two chromosomes are combined by crossover. Two parent chromosomes are each cut at a random location and the opposing sections rejoined to form two children:

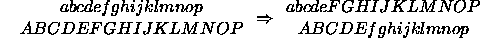
In addition a small amount of mutation is introduced, randomly changing bits in the chromosomes.

The algorithm starts by creating a first generation of N chromosomes scattered randomly about the search space. Each new generation is produced as follows

• Decode each chromosome to obtain a and evaluate .
• Rank the chromosomes by their function evaluation
• Use some breeding strategy to combine good chromosomes and discard bad ones, allowing the better chromosomes to breed with a greater probability. This generates a new set of N individuals.
• Apply a small amount of mutation to the chromosomes.

The assumption is made that the optima can be formed by combining small sub-sections of the chromosomes, each of which will tend to improve the function evaluation of any full chromosome containing them. Thus these good building blocks will tend to be reproduced and will propagate through the population. Eventually all the current generation of individuals should end up in the global optimum.

For functions of the form 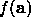where each 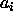is continuous with upper and lower bounds a straightforward bitstring encoding of a is sufficient for the chromosomes. However, permutation problems (such as the Travelling Salesman Problem) are much harder - Simulated Annealing algorithms are likely to give better results.

Under the right conditions Genetic Algorithms have been shown to converge to good solutions remarkably quickly and have the advantage that the rate of convergence varies in accordance with the complexity of the search space [4] [15] [17].