Final-year Geometric Modelling Course

1993 Exam

1

Answers to each part of this question should be brief: a sentence or two, or a quick sketch. (1 mark for each part)

  1. What is depth cuing?
  2. Show how a wire-frame `model' can be ambiguous.
  3. Show how a face `model' can represent a non-solid object.
  4. What is the difference between a face `model' and a boundary-representation model?
  5. What is the difference between a boundary-representation model and a set-theoretic (that is a CSG) model?
  6. Show how an arbitrarily small geometrical change can change the topology of a boundary-representation model.
  7. The extended Euler-Poincaré formula is . If a faceted boundary model of a single object has 14 faces, 24 vertices, 4 rings, and 36 edges, how many holes are there in it?
  8. Sketch an object that would satisfy the constraints of the last question.
  9. Very briefly describe the winged-edge data structure.
  10. Why is it hard to compute the volume of a boundary model, but easy to compute its surface area?
  11. Why is it easy to compute the volume of a set-theoretic model, but hard to compute its surface area?
  12. How might a picture of a boundary model be obtained?
  13. How might a picture of a set-theoretic model be obtained?
  14. How does a NURBS differ from a B-spline?
  15. Why is it important that the Bernstein basis functions should add up to 1?
  16. Give two problems that may arise when sculptured surfaces are used to model real engineering components.
  17. In feature recognition, what is destructive solid geometry?
  18. How can a membership test be done in a boundary-representation modeller?
  19. Sketch the solid volume that an end mill in a vertical-axis milling machine sweeps as it moves in a straight line in x and y.
  20. What are attributes in a geometric modeller?


2

Figure Q2 shows a con-rod from an internal combustion engine. A set-theoretic modeller with (among other things) cuboids and bounded cylinders (that is, cylinders with ends) as primitives is going to be used to model the con-rod. Construct a set-theoretic expression for the con-rod, describing (with the aid of sketches, if need be) which primitives are which parts of the con-rod. (14 marks)

The con-rod is to be made by forging. How might the mass of the steel blank that will be forged into its shape be estimated from the model? Assume that no material will be lost as flash or in other ways. (6 marks)

3

Using interval arithmetic, find out if the axis-aligned rectangle with corners at (-1,-1), (2,4) is wholely inside or wholely outside the region defined by the two-dimensional polynomial inequality , or if it might cut across the region's boundary. (12 marks)

What use does this technique have in dealing with three-dimensional set-theoretic geometric models? (8 marks)

4

The formula for a Bézier curve, , is:

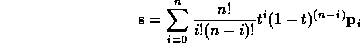
Show that for the four-point control track {(1,1), (2,2), (3,1), (3,3)} the formula gives the same curve-point at 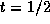as the De Casteljau construction. (12 marks)

A general parametric quadratic curve in space is , where is the point on the curve at t, , and the 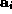are vector coefficients, . Describe how you might find the closest point on the curve to a point, 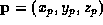. (5 marks)

What problems might your method have if the degree of the curve was higher? (3 marks)

5

A simple boundary-representation modeller is to be used to represent faceted single objects with no holes. Using any computer language, describe a data structure that might be used to hold such a model (10 marks) and say how this might be checked for solidity against a simplified version of the formula in question 1.7 (5 marks).

Show how a cuboid would be represented in your data structure. (5 marks)

Back to: Final-year Geometric Modelling Course Exams

© Adrian Bowyer 1996