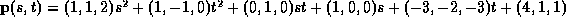Final-year Geometric Modelling Course
1994 Exam
1
Answers to each part of this question should be brief: a sentence
or two, or a quick sketch. (1 mark for each part)
- What is the haloing method of depth cuing?
- How does the depth buffer make pictures of three-dimensional
objects?
- The simple version of the Euler-Poincaré formula is F+V-E = 2.
Draw a shape for which the formula is valid and show that
it is.
- Draw a shape for which the simple Euler-Poincaré formula is not
valid, and show that it isn't.
- What is an Euler operator in a B-rep geometric modelling program?
- Why are curved shapes slightly problematical for B-rep modellers?
- What is a duct-type modeller?
- What sort of shapes can duct-type modellers model well?
- What is the difference between a Bézier curve and a B-spline?
- What is the difference between a B-spline and a NURBS?
- In a design, it is important that a simple-shaped moving part does
not hit a panel that is represented by a NURBS patch. What
easy test would ensure that no collision occured?
- What are twist vectors in parametric patches?
- How could you estimate the volume of a set-theoretic (or CSG)
geometric model?
- How can the difference operator be removed from set-theoretic models?
- What is recursive spatial division?
- Why is interval arithmetic useful with solids represented by implicit
inequalities?
- What is the backwards-growing feature recognition technique?
- Why are tolerances problematical for geometric modellers?
- A slot-drill (a type of cylindrical cutter) moves in a circular
arc in a vertical-axis milling machine. What shape would it sweep out?
- Are most commercial geometric modellers B-rep or set-theoretic?
2
Explain how the implicit equation for a two-dimensional ellipse can
be constructed from the implicit straight-lines that form its major and minor
axes. (4 marks) Why is this construction advantageous when it comes to
translating or rotating the ellipse? (2 marks)
A prolate spheroid (or rugby ball, if you prefer...)
needs to be modelled in a geometric modeller, as it is the shape of the
cavity in a machine being designed to mold gel vitamin capsules.
The major axis of the spheroid is 12mm long, and its minor axis is
8mm long. The major axis lies along the vector 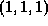 , and the
centre of the spheroid is the origin of coordinates. Using the method
that you described in answer to the first part of this question, construct
an implicit equation for the spheroid in three dimensions. Don't bother
to multiply the equation out. (8 marks)
, and the
centre of the spheroid is the origin of coordinates. Using the method
that you described in answer to the first part of this question, construct
an implicit equation for the spheroid in three dimensions. Don't bother
to multiply the equation out. (8 marks)
A section through the machine is being pictured by a ray-tracing program.
Where (if it does at all) does the ray x = 10 - 10t, y = 10 - 10t, z = t
strike the spheroid? (6 marks)
3
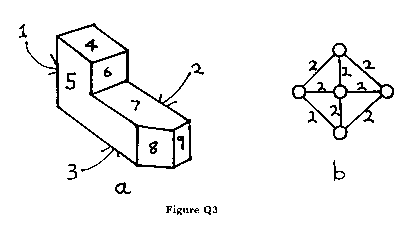
The object shown in Figure Q3.a has nine faces (as numbered; faces 1, 2, and
3 being hidden from view). Using the conventions that a concave edge
has the value 1 and a convex edge has the value 2, construct the face
adjacency graph (8 marks) and the face adjacency matrix (4 marks)
for the object.
Figure Q3.b shows a pattern in the form of a face adjacency graph of
a feature that is to be
searched for in the object. What sort of shape is the feature? (Make a
sketch - 5 marks.) Ring (ideally using a different colour than the one
you're writing everything else with) one occurence of the feature in your
face adjacency graph for the original object. (3 marks)
4
A parametric quadratic patch:
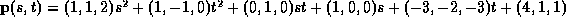
is to be cut with a ball-nosed cutter of radius 0.5. Where is the
centre of the cutter when it is cutting the patch at s=0, t=0 and also when
it is at s=0, t=1? (Assume that the vector-product of gradients in
the s and t directions in that order points from
solid to air.) (12 marks)
If the patch were being cut, what calculations
would need to be done to ensure that the tool was not gouging parts of the
surface that should have been preserved. (No need for formulae - 8 marks)
5
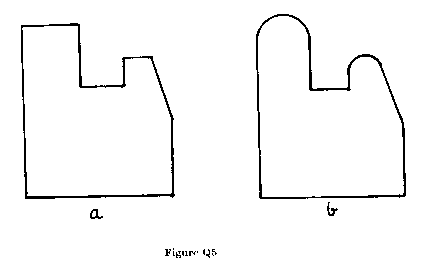
Describe, using the shape shown in Figure Q5.a as an example, how a
two-dimensional straight-edged drawing can be decomposed into convex
regions. (8 marks)
How does this help with the problem of user-input to geometric modellers?
(3 marks)
Could the method be extended to cover circular arcs such as those in
Figure Q5.b? (6 marks) What problems would you anticipate with allowing
curved edges in general? (3 marks)
Back to:
Final-year Geometric Modelling Course Exams
©
Adrian Bowyer 1996
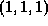 , and the
centre of the spheroid is the origin of coordinates. Using the method
that you described in answer to the first part of this question, construct
an implicit equation for the spheroid in three dimensions. Don't bother
to multiply the equation out. (8 marks)
, and the
centre of the spheroid is the origin of coordinates. Using the method
that you described in answer to the first part of this question, construct
an implicit equation for the spheroid in three dimensions. Don't bother
to multiply the equation out. (8 marks)