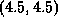, for example].
Answers to each part of this question should be brief: a sentence or two, or a quick sketch. (1 mark for each part)
Figure Q2 (you should have two copies: one for rough
work, one for neat; hand both in) shows a design for the supports of a
semi-cylindrical cover for a walkway outside a new building.
All the corners of the shape are deliberately placed at coordinate values
that are odd multiples of 0.5 [thus the sharp corner formed by the two
arcs is at 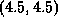, for example].
).
You may need extra inequalities and also to use
the complements of some in order to chop chunks off at the right
places. (5 marks)
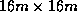square into rectangular regions
(each rectangle being half the area of its parent) such that
each leaf rectangle contains
at most two of the original seven primitives. (5 marks)
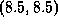is inside the area of the support. Prove
this using a simple set-theoretic expression that only describes
the support inside your leaf rectangle containing that
point. (5 marks)
Don't forget to write your candidate number on both Figure Q2s and to hand them in with your script...
Several quadratic parametric Bézier curves in the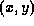 
plane
are to be used to define a cross-section of an aerofoil.
One such curve has a
control track consisting of three
points,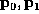 
, and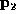 
. Draw a diagram showing
De Casteljau's construction of the curve, and from it derive the equation
of the curve with a parameter t that is 0 at one end and 1 at the
other. (10 marks)
Show that the functions of the parameter, t, that multiply
each point on the control track (that is, the weight applied
to each control-track point) can be
derived from the expansion of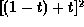 
(which, of course,
equals 1). (5 marks)
How would you ensure that two such curves joined end-to-end did so smoothly (that is to say, had a common tangent at their join)? (2 marks)
In order to compute the lift and drag of the aerofoil it is necessary (among other things) to be able to find the gradient of the curves at any point along them. Given a value of t along one curve, how would you find a normal vector to the curve at that point? (3 marks)
A geometric model can be complicated in two different ways: it can have a large number of projections, holes, and so on compared with a simple model, or it can have few of these but they can have complicated curving surfaces (that is, surfaces of high degree) as opposed to low-degree ones. Both types of complexity may occur together in some models, of course.
Write a description of the kinds of problems these two types of complexity cause both B-rep and set-theoretic geometric modelling programs (5 marks), and describe the ways in which such programs may overcome them (15 marks).
A flat plane in space is
represented by the implicit equation a x + b y + c z + d = 0; it forms
part of the surface of a geometric model. A picture of the model is to
be rendered on a computer using a ray-tracing program. A
straight ray in space is represented by the parametric equation
.
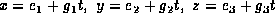Derive the equation which gives
the value of t where the ray cuts the plane. (6 marks)
Using FORTRAN or any other computer language write a subroutine RAYT to compute the t value, T, where the ray hits the plane. The subroutine should also return an INTEGER value HIT which is 0 if the ray misses completely (that is, if it is parallel to the plane) or 1 if it strikes the plane. If you choose to use FORTRAN your subroutine should start like this:
SUBROUTINE RAYT(A,B,C,D,E,G,T,HIT)
REAL A,B,C,D,E(3),G(3),T
INTEGER HIT
where A, B, C, and D are the plane's coefficients, E the three coordinate values of the start of the ray, and G the three corresponding gradient values for the ray. You may need to declare other variables to hold the results of intermediate calculations. (12 marks)
Given T, how would you find the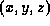 
coordinates in space
where the ray struck the plane? (2 marks)
© Adrian Bowyer 1996