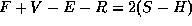 . What
do the variables mean?
. What
do the variables mean?
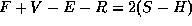 . What
do the variables mean?
. What
do the variables mean?
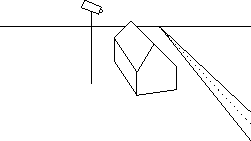
Figure Q2
Figure Q2 shows a traffic surveillance camera, the road that it is surveying, and a bank that does not yet exist but which it is proposed to build. The bank's architects are investigating potential obstructions to the camera's lines of sight. The bank is held as a set-theoretic geometric model in a CAD system. The outside walls and roof are extracted from this; they are described by the inequalities:

All units are in metres. The set-theoretic expression for the bank
building (ignoring the floor) is 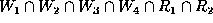 .
The camera is at the point
.
The camera is at the point 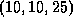 . Calculate if
it can see the point
. Calculate if
it can see the point 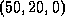 on the road. (11 marks)
on the road. (11 marks)
How would things become more complicated if some walls of the bank were curved? (Give a brief numerical example in your answer.) (4 marks)
The bank is built. A gang of bank robbers hack into the architects' CAD system and copy the complete detailed final geometric model, which includes data on the positions of the bank's internal security cameras. Describe how the gang could make pictures of the room containing the bank vault that would show them what parts of the room the security cameras could and couldn't see, and what parts of the room the traffic camera could and couldn't see through the windows. (5 marks)
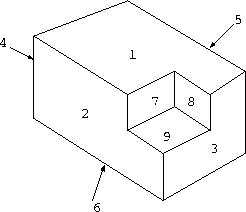
Figure Q3
Figure Q3 shows a block with numbered faces (faces 4, 5, and 6 being invisible from the viewpoint) that is held in a B-rep modeller. Construct a face-adjacency graph for the block (4 marks). Construct a template graph for the indentation and mark where it appears on the larger graph (2 marks). Construct a template graph for a rectangular hole that might go right through a component (6 marks). Explain how these sorts of graphs and their closely-related face-adjacency matrices (give examples of these) help with the problems of feature recognition (8 marks).
Two nearly-parallel straight lines are represented by the equations
Ax + By + C = 0 and 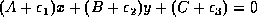 . The epsilons are small, and may be positive or negative. What are
the coordinates of the lines'
intersection point (5 marks)? What effect will small changes in the values of
the epsilons have on them? (Draw pictures to illustrate your answer.)
(7 marks) Comment on the difficulties
that problems of this sort pose in geometric modellers and how they may
be alleviated by both careful programming and by changes in the
way that the computer is instructed to do arithmetic (8 marks).
. The epsilons are small, and may be positive or negative. What are
the coordinates of the lines'
intersection point (5 marks)? What effect will small changes in the values of
the epsilons have on them? (Draw pictures to illustrate your answer.)
(7 marks) Comment on the difficulties
that problems of this sort pose in geometric modellers and how they may
be alleviated by both careful programming and by changes in the
way that the computer is instructed to do arithmetic (8 marks).
Explain how the volume and the centroid of both a set-theoretic and a B-rep geometric model might be found (6 marks).
Components which are being represented using a geometric modeller will be brought to a robot on a conveyor belt. Before they are picked up by the robot, a TV camera sends an image of them taken directly from above to the robot's controlling computer.
Given a procedure that will compute the 3D convex hull of the models, how could the stable configurations that each object that they represent might rest in on the flat conveyor be found? (6 marks) Give two ways for generating synthetic images of the models that the controlling computer could compare with the TV images to find out which way up the real components were resting. (4 marks)
What problems would there be with models with curved surfaces? (4 marks)
© Adrian Bowyer 1996