Final-year Geometric Modelling Course
1999 Exam
1
Answers to each part of this question should be brief: a sentence
or two, or a quick sketch. [1 mark for each part]
-
Show how a wire-frame `model' can be ambiguous.
-
How does the depth buffer make pictures of three-dimensional objects?
-
What is the haloing method of depth cuing?
-
The simple version of the Euler-Poincaré formula is F+V-E = 2.
Draw a shape for which the formula is valid and show that it is.
-
The extended Euler-Poincaré formula for checking topological consistency
in a B-rep modeller is
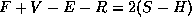 .
What do all the variables mean?
.
What do all the variables mean?
-
What is the difference between a boundary-representation model and a set-theoretic
(that is a CSG) model?
-
What is an Euler operator in a B-rep geometric modelling program?
-
Why are some curved shapes slightly problematical for B-rep modellers?
-
What are the differences between a B-spline and a NURBS?
-
In a design, it is important that a simple-shaped moving part does not
hit a panel that is represented by a NURBS patch. What easy test would
ensure that no collision occurred?
-
Why is it hard to compute the volume of a boundary model, but easy to compute
its surface area?
-
Why is it hard to compute the surface-area of a set-theoretic model, but
easy to compute its volume?
-
What is a membership test?
-
Why is it important that the Bernstein basis functions should add up to
1?
-
How can the difference operator be removed from set-theoretic models?
-
How does the Monte Carlo method of finding the volume of a geometric
model work?
-
What is recursive spatial division?
-
Why is interval arithmetic useful with solids represented by implicit inequalities?
-
A slot-drill (a type of cylindrical cutter) moves in a horizontal straight
line in a vertical-axis milling machine. What shape would it sweep out?
-
Why are tolerances problematical for geometric modellers?
2
The formula for a Bézier patch is:
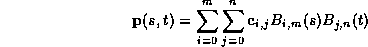
where
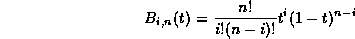
A Bézier patch has 9 control points, 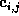 ,
arranged in a
,
arranged in a 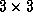 grid in space.
The control points are conventionally numbered
grid in space.
The control points are conventionally numbered 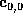 up to
up to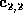 . Sketch the weighting functions
for the point
. Sketch the weighting functions
for the point 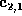 . [10 marks]
. [10 marks]
Show what calculations would need to be done to offset a ball-nosed
cutter of radius r from the patch at 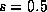 ,
, 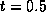 .
[10 marks]
.
[10 marks]
3
A set theoretic geometric model of an object has the following implicit
inequalities as primitives (all units in mm):
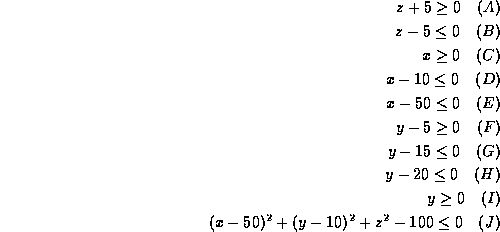
and the set-theoretic expression describing the object is:
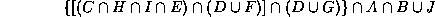
-
Draw a sketch of the object. [6 marks]
-
What is the length, width, and height of the object in the x, y,
and z directions? [4 marks]
-
Is the point (42, 4, 0) inside the object or outside it (prove this - don't
just rely on plotting on your sketch)? [10 marks]
4
The crinkliness of a three-dimensional object is a measure of how
much it differs from a sphere. It is defined as the ratio between the surface
area of the object and the surface area of the sphere with the same volume
as the object. A sphere itself thus has a crinkliness of 1; everything
else has a value that is bigger, with a cube giving a smaller value than
a brick, which in turn gives a smaller value than a starfish.
Describe in detail how you would compute the crinkliness of a boundary-representation
geometric model. (Reminder: the volume of a sphere is 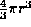 and its area is
and its area is 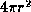 .) [10 marks]
.) [10 marks]
A company has a large collection of new geometric models that are the
designs for the component parts of a machine that it proposes to manufacture
and to market. It further proposes to use the crinkliness statistic as
a rough measure to help estimate the relative costs of manufacturing the
components both by machining and by other processes such as injection moulding.
Comment on the strengths and weaknesses of this proposal. [10 marks]
5
Explain, with the aid of sketched examples, the face adjacency graph
and its use in feature recognition. [10 marks]
Show the patterns needed to search the graph for:
-
A through hole that is triangular in cross-section, [3 marks]
-
A rectangular projecting lug, [3 marks]
-
And a flat-bottomed depression that is hexagonal in cross-section. [4 marks]
Back to:
Final-year Geometric Modelling Course Exams
©
Adrian Bowyer 1996
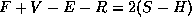 .
What do all the variables mean?
.
What do all the variables mean?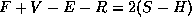 .
What do all the variables mean?
.
What do all the variables mean?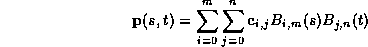
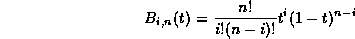
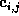 ,
arranged in a
,
arranged in a 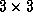 grid in space.
The control points are conventionally numbered
grid in space.
The control points are conventionally numbered 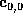 up to
up to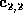 . Sketch the weighting functions
for the point
. Sketch the weighting functions
for the point 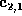 . [10 marks]
. [10 marks]
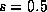 ,
, 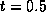 .
[10 marks]
.
[10 marks]
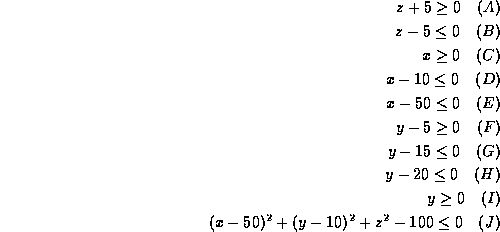
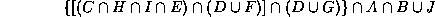
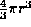 and its area is
and its area is 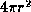 .) [10 marks]
.) [10 marks]