 and
and 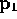 in the
in the  plane, and you form a third point:
plane, and you form a third point:
Suppose you are given the positions of two points  and
and 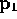 in the
in the  plane, and you form a third point:
plane, and you form a third point:
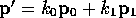
where 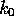 and
and 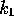 are any constants. What constraints (if
any) are there on the position of
are any constants. What constraints (if
any) are there on the position of 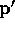 ?
?
Suppose that  ; where can
; where can 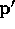 lie now?
lie now?
Suppose, in addition, that 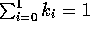 ;
what positions can
;
what positions can 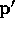 take up now?
take up now?
Finally, consider the equation
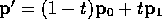
where 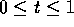 . As t varies, what happens to
. As t varies, what happens to 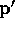 ?
?
Now we add a third point, 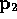 ; where can
; where can 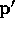 be
if
be
if

and

Now another pawl on the ratchet; we invent two new  s with
subscripts. The first one takes the place of the old
s with
subscripts. The first one takes the place of the old 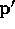 :
:
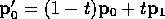
and the second relates 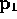 and
and 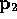 in the same way:
in the same way:

Finally 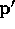 overarches them:
overarches them:
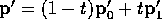
Again, as t varies between 0 and 1, what does 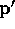 do?
do?
Making---at last---the leap to an arbitrary number of points,
suppose we have n+1 of them in fixed positions, and also
n+1 scalar values 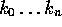 (which we shall call
weights). As before
(which we shall call
weights). As before 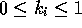 and
and

So we form 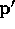 as
as

What now is the locus of  ?
?
Finally, another tack. Temporarily considering t and 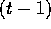 to
be completely unrelated variables, what is the binomial expansion of:
to
be completely unrelated variables, what is the binomial expansion of:
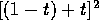
and of

What are they both equal to?
© Adrian Bowyer 1996