Warnock's rendering algorithm, and ray-tracing
Warnock's rendering algorithm

Warnock's algorithm works by dividing up the rectangle of the screen upon which the picture is to be rendered. The components of the geometric model (or other representation) to be depicted are projected onto the screen-rectangle and counted. If there are more of them than a pre-determined small number (usually about four or five) then the screen is divided into four similar rectangles and the counting process is repeated recursively.
In this way large simple areas of the screen can be coloured in quickly (with blue for the sky, for example) and areas into which complicated bits of model project are found. Once the count for a rectangle is small a process like the painter's algorithm is used to render it, being, of course, made much simpler by the reduced count of entities to be dealt with.
In areas of irreducible complexity (which are usually rare, even for very complicated scenes) then the process divides down to individual pixels, and these can be rendered using a ray tracer (see the next item).
Ray-tracing
Ray-tracing is perhaps the simplest method of making a picture on a computer that there is. It is also very powerful, being able to simulate shadows, reflections, aerial perspective and mist, refractions and a host of other optical effects familiar to us in the everyday world but impossible or very hard for some of the other rendering methods that we have encountered to handle. Why, then, is it not universally used? The answer is that, though it is childishly easy to write an inefficient slow ray-tracing program, it is very hard to write an efficient fast one.
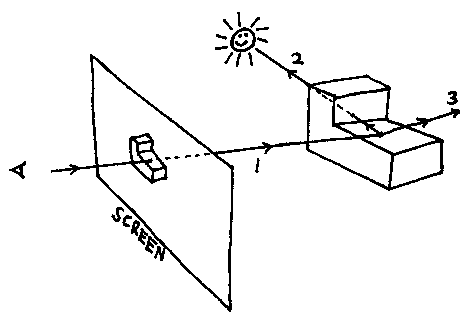
Ray-tracing works by imagining a ray (1) running from the viewer's eye position through every pixel on the screen. The rays are traced back to find the first surface of the geometric model that they strike. This surface decides the colour of the corresponding pixel. It's like tracing light backwards.
But there is no need to stop there. Once the point on the model where a ray strikes has been found another ray (2) can be run off to the source of illumination. If it hits something on the way, the original point is in shadow, if not the point is brightly illuminated. It is just as easy to deal with multiple light sources giving all sorts of fancy penumbra effects.
A reflected ray (3) can be generated and run to see what it hits, thus simulating mirrored surfaces. If the screen pixel is made more grey the longer the ray is before it hits something, then the scene appears to be shrouded in mist. Below is a ray-traced picture of part of an oil refinery generated by the svLis geometric modeller.

And here is exactly the same scene rendered by the same ray-tracing program with the mist option turned on. (I should have remembered to turn the shadows off...)

We have already seen how Lambert's cosine law can allow us to shade a matt surface by making the brightness of the surface proportional to the cosine between the light vector and the surface's normal vector.

In order to simulate shinyness we add in an extra component.
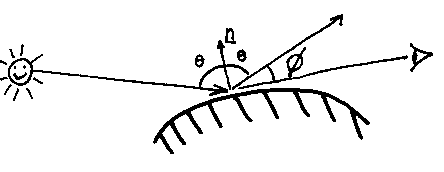
The surface intensity, I, now has a Lambert's-law component and an extra one that is proportional to the closeness of the eyeline to the reflected ray:
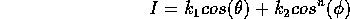
The ks are constants, as is the n. The bigger n is, the shinier the surface will appear.
The Lambert's colour should be the surface colour, and the reflected colour should be the light's colour (which is not always white, of course). This specular reflection is a bit of a cheat, with (unlike Lambert's law) little justification in real physics. But it looks OK...
© Adrian Bowyer 1996