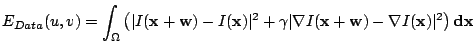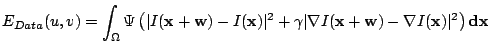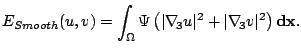The Variational Model

Before deriving a variational formulation for our optical flow method, we give an intuitive idea of which constraints in our view should be included in such a model.

• Grey value constancy assumption.
  Since the beginning of optical flow estimation, it has been assumed that the grey value of a pixel is not changed by the displacement.

  $$I(x,y,t) = I(x+u,y+v,t+1)$$ (1)

  
  
  Here $I:\Omega\subset\mathbb{R}^3\rightarrow\mathbb{R}$ denotes a rectangular image sequence, and $\mathbf w:=(u,v,1)^\top$ is the searched displacement vector between an image at time $t$ and another image at time $t+1$. The linearised version of the grey value constancy assumption yields the famous optical flow constraint [11]

  $$I_xu+I_yv+I_t = 0$$ (2)

  
  
  where subscripts denote partial derivatives. However, this linearisation is only valid under the assumption that the image changes linearly along the displacement, which is in general not the case, especially for large displacements. Therefore, our model will use the original, non-linearised grey value constancy assumption (1).

  
  

• Gradient constancy assumption.
  The grey value constancy assumption has one decisive drawback: It is quite susceptible to slight changes in brightness, which often appear in natural scenes. Therefore, it is useful to allow some small variations in the grey value and help to determine the displacement vector by a criterion that is invariant under grey value changes. Such a criterion is the gradient of the image grey value, which can also be assumed not to vary due to the displacement [18]. This gives

  $$\nabla I(x,y,t) = \nabla I(x+u,y+v,t+1).$$ (3)

  
  
  Here $\nabla=(\partial_x,\partial_y)^\top$ denotes the spatial gradient. Again it can be useful to refrain from a linearisation. The constraint (3) is particularly helpful for translatory motion, while constraint (2) can be better suited for more complicated motion patterns.

  
  

• Smoothness assumption.
  So far, the model estimates the displacement of a pixel only locally without taking any interaction between neighbouring pixels into account. Therefore, it runs into problems as soon as the gradient vanishes somewhere, or if only the flow in normal direction to the gradient can be estimated (aperture problem). Furthermore, one would expect some outliers in the estimates. Hence, it is useful to introduce as a further assumption the smoothness of the flow field. This smoothness constraint can either be applied solely to the spatial domain, if there are only two frames available, or to the spatio-temporal domain, if the displacements in a sequence of images are wanted. As the optimal displacement field will have discontinuities at the boundaries of objects in the scene, it is sensible to generalise the smoothness assumption by demanding a piecewise smooth flow field.

  
  

• Multiscale approach.
  In the case of displacements that are larger than one pixel per frame, the cost functional in a variational formulation must be expected to be multi-modal, i.e. a minimisation algorithm could easily be trapped in a local minimum. In order to find the global minimum, it can be useful to apply multiscale ideas: One starts with solving a coarse, smoothed version of the problem by working on the smoothed image sequence. The new problem may have a unique minimum, hopefully close to the global minimum of the original problem. The coarse solution is used as initialisation for solving a refined version of the problem until step by step the original problem is solved. Instead of smoothing the image sequence, it is more efficient to downsample the images respecting the sampling theorem, so the model ends up in a multiresolution strategy.

With this description, it is straightforward to derive an energy functional that penalises deviations from these model assumptions. Let $\mathbf x:=(x,y,t)^\top$ and $\mathbf w:=(u,v,1)^\top$. Then the global deviations from the grey value constancy assumption and the gradient constancy assumption are measured by the energy

$$E_{Data}(u,v) = \int_\Omega \left(\vert I(\mathbf x+ \mathbf w)-I... ...rt\nabla I(\mathbf x+ \mathbf w)-\nabla I(\mathbf x)\vert^2\right) \mathbf {dx}$$ (4)

with $\gamma$ being a weight between both assumptions. Since with quadratic penalisers, outliers get too much influence on the estimation, an increasing concave function $\Psi(s^2)$ is applied, leading to a robust energy [6,12]:

$$E_{Data}(u,v) = \int_\Omega \Psi\left(\vert I(\mathbf x+ \mathbf ... ...ert\nabla I(\mathbf x+\mathbf w)-\nabla I(\mathbf x)\vert^2\right) \mathbf {dx}$$ (5)

The function $\Psi$ can also be applied separately to each of these two terms. We use the function $\Psi(s^2)=\sqrt{s^2+\epsilon^2}$ which results in (modified) $L^1$ minimisation. Due to the small positive constant $\epsilon$, $\Psi(s)$ is still convex which offers advantages in the minimisation process. Moreover, this choice of $\Psi$ does not introduce any additional parameters, since $\epsilon$ is only for numerical reasons and can be set to a fixed value, which we choose to be $0.001$.
Finally, a smoothness term has to describe the model assumption of a piecewise smooth flow field. This is achieved by penalising the total variation of the flow field [15,8], which can be expressed as

$$E_{Smooth}(u,v) = \int_\Omega \Psi\left(\vert\nabla_{\hspace*{-0.5mm}3}u\vert^2+\vert\nabla_{\hspace*{-0.5mm}3}v\vert^2\right) \mathbf {dx}.$$ (6)

with the same function for $\Psi$ as above. The spatio-temporal gradient $\nabla_{\hspace*{-0.5mm}3}:=(\partial_x, \partial_y, \partial_t)^\top$ indicates that a spatio-temporal smoothness assumption is involved. For applications with only two images available it is replaced by the spatial gradient.
The total energy is the weighted sum between the data term and the smoothness term

$$E(u,v) = E_{Data} + \alpha E_{Smooth}$$ (7)

with some regularisation parameter $\alpha > 0$. Now the goal is to find the functions $u$ and $v$ that minimise this energy.