


Next: Model selection when sensor
Up: Model selection in computer
Previous: Intuition
Several model selection criteria have been used in computer vision, and many
more have found popularity in the statistics literature. Model
selection criteria based on Chi-square test and F-test have been used
both in the vision and statistics literature [5,19].
More recently, information theoretic model selection criteria have gained
increasing popularity.
Information theoretic criteria are mainly based on Bayes rule,
Kullback-Leibler (K-L) distance, and minimum description lengths
(MDL). Criteria based on
Bayes rule choose the model that maximizes the probability of the data,
D, given the model m and prior information I. This probability
is given by
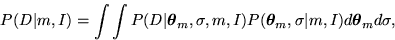
where  is the
is the  parameter vector for model
m, and
parameter vector for model
m, and 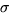 is
the standard deviation of sensor noise. The first term in the above integral
is just the likelihood
is
the standard deviation of sensor noise. The first term in the above integral
is just the likelihood  , and
, and  is the prior probability of
is the prior probability of  and
and 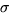 . Several
Bayesian criteria have been derived depending on the choice of
priors [10,11,13].
One such criteria chooses the model that maximizes [6,5]
. Several
Bayesian criteria have been derived depending on the choice of
priors [10,11,13].
One such criteria chooses the model that maximizes [6,5]
|  |
(1) |
where  is the Hessian of
is the Hessian of  . Another set of
model selection criteria minimize the K-L distance between the candidate
model's fit and the generating model's fit, given by
. Another set of
model selection criteria minimize the K-L distance between the candidate
model's fit and the generating model's fit, given by

But evaluating the above distance is not possible, since it requires knowledge
of the actual model parameters 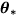 . A number of model
selection criteria have been derived based on approximations to this distance.
The most common of these criteria are AIC and CAIC, and are given by
. A number of model
selection criteria have been derived based on approximations to this distance.
The most common of these criteria are AIC and CAIC, and are given by

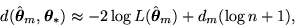
respectively. Finally, MDL based criteria minimize the number of bits
required to represent the data using model m given by
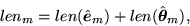
where the two terms give the number of bits required to encode the
residuals and the estimated parameter vector, respectively. A popular MDL
criteria is due to Rissanen, and is given by
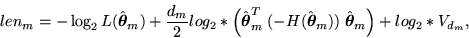
where 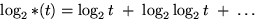 ,including only its positive terms, and Vdm is the volume of the
dm-dimensional unit hypersphere (see [7, page 24]).
,including only its positive terms, and Vdm is the volume of the
dm-dimensional unit hypersphere (see [7, page 24]).
An advantage of these criteria is the ease with which they can be used.
There is no problem of specifying empirical thresholds, significance levels,
or the need to reference look up tables. However, these criteria require
fitting all the models to the data, which may be expensive and unnecessary in
many applications.
Although these criteria
start from different premises, interestingly, they
all appear in the form of a penalized likelihood and optimize
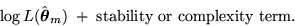
Further, criteria formulated using one premise have often been derived later
using other premises.
However, all these criteria assume data contaminated only by small scale
random errors. But vision data is also contaminated with outliers.
Several modifications have been recently proposed to the above criteria
in order to incorporate outliers [3,8,14,15,16,17,18].



Next: Model selection when sensor
Up: Model selection in computer
Previous: Intuition
Kishore Bubna
10/9/1998
![]()
![]()
![]()
![]()
![]()
![]()
![]()