Cost Function

The IPAN Tracker uses the cost function introduced by Sethi and Jain in [11]. This function is defined in equation (1).

The post-processing search area $S^+_{e}$ introduced in section 4.3 (figure 3) is obtained by separately applying the cost limit $\delta_{max}$ to the two terms of the cost function. The first term then limits the direction as $\theta \in \left[ \theta_1,\theta_2 \right]$; the second term, combined with the speed limit $v_{max}$, constrains the speed as $v\in \left[ v_1,v_2\right] \cap \left[ 0,v_{max}\right]$.

As discussed in section 4.3, less deviation from smoothness is allowed for a hypothetical occluded point than for an actually observed point. Mathematically, directional continuity of broken trajectories is enforced by limiting in (1) the unweighted rather than weighted terms. Under these constraints, it is easy to derive that
$$\begin{align*}\theta_{1,2} & = \theta_e \mp \arccos (1-\delta_{max}) \\ % v_{1,2... ...x}(2-\delta_{max})} \right)^2}% { \left( 1-\delta_{max}\right)^2 } \end{align*}$$
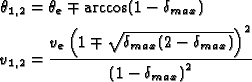
Here $\theta_e$ is the direction, $v_{e}$ the magnitude of the incoming velocity vector $\vec{v_{e}}$.

From these equations, the maximum allowed direction change for broken trajectories is $\pi /2$, when $\delta_{max}= 1$. When $\delta_{max}= 0.5$, the turn limit is $\pi /3$. $0 \leq v_{1} \leq v_{e}$, while $v_{2} \geq v_{e}$. When $\delta_{max}$ is set close to $1$, $v_{1} \approx 0$ and $v_{2} \gg v_{e}$.

Expressions for $S^-_{s}$ are obtained in the same way.