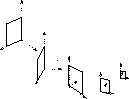
Figure 1: example of critical motion : vertical rotation axis
Horizontal rotation axis. We have 
and so, 
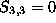and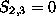 
(see eq:Sx) : eq:sys3 gives 
and 
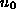and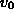 
can then be computed with eq:sys5 and eq:sys6.
if we impose r=0, eq:sys2 gives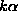 
. However, eq:sys1 can't give either 
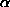or 
.
if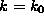 
is considered, 
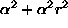and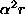 
can be calculated directly and solved to give r, 
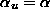and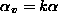 
.
Vertical rotation axis. This is the case when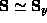 
, which is similar to the previous one. We have 
.
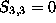if r=0, we have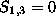 
and then all parameters except k and 
can be evaluated.
if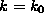 
, 
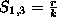leads to a total resolution of calibration
Rotation axis orthogonal to the image plane. We have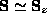 
(
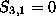and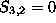 
).
It is the worst critical case in so far as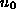 
, 
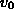, k and r can be calculated, but 
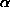remains always undetermined, whatever the constraint may be.
As a conclusion, we saw that the problem of affine-to-Euclidean calibration could be easily solved in particular cases (single motion, all parallel axes rotations
).
We also showed that using the constraint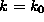 
allowed us to avoid critical cases : there remains then just one real critical motion (rotation axes orthogonal to the image plane).