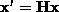Estimate 
for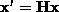 
,
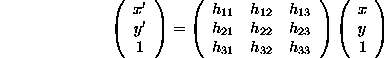
where = is equality up to scale. Minimum number of correspondences: 4 points (non-collinear) or 4 lines (non-concurrent).
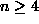correspondences
n = 4 will be covered as a special case.
Each point correspondence generates two linear equations for
the elements of 
(dividing by the third component
to remove the unknown scale factor)
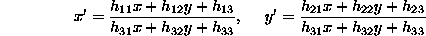
and multiplying out
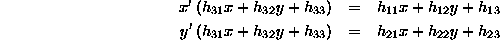
Then 
points generates 2 n linear equations,
which are sufficient to solve for 
.
The problem with projective transformations is that
the matrix 
is only recovered up to scale.
Homogeneous Solutions There are two methods of dealing with the unknown scale factor in a homogeneous matrix
.
Method I
If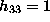 
, then the above equations can be written:
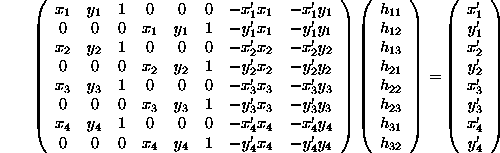
for 4 points. A linear solution is then obtained, in the usual manner, by solving the set of linear simultaneous equations. Similarly, for n > 4 points, a solution can be obtained using a pseudo-inverse.
The problem with this approach is that if the true solution
is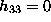 
, then this cannot be reached. Consequently,
a poor quality estimate of 
will be obtained.
Method II
The equations,
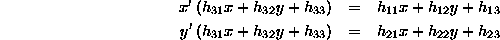
can be rearranged as
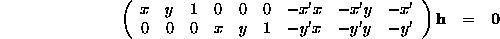
where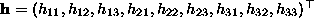 
is the matrix 
written
as a vector.
For 4 points,
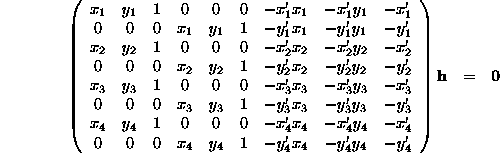
which has the form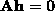 
, with
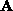a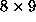 
matrix. The solution
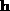is the (one dimensional) kernel of 
.
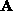For n > 4 real point correspondences,
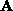is a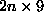 
matrix,
and there will not be a solution to
. In this case, a sensible procedure
is to again minimise the residuals. It can be shown that
the vector that minimises 
subject
to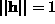 
,
is the eigenvector with least eigenvector of 
.
In the case of n = 4 the least eigenvalue is zero, and the
eigenvector is the kernel of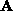 
.