Epipolar Geometry

The fundamental geometric relationship between two perspective cameras.

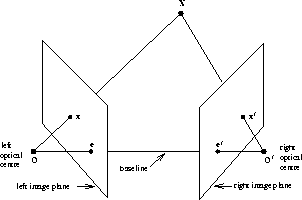
• The epipole: is the point of intersection of the line joining the optical centres---the baseline---with the image plane. The epipole is the image in one camera of the optical centre of the other camera.

  

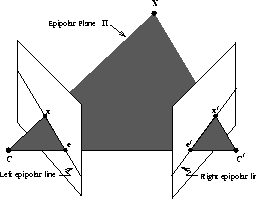
• The epipolar plane: is the plane defined by a 3D point and the optical centres. Or, equivalently, by an image point and the optical centres.

• The epipolar line: is the straight line of intersection of the epipolar plane with the image plane. It is the image in one camera of a ray through the optical centre and image point in the other camera. All epipolar lines intersect at the epipole.

Epipolar pencil

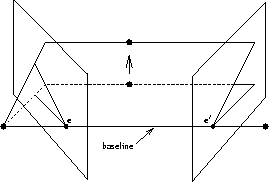
As the position of the 3D point 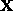varies, the epipolar planes ``rotate'' about the baseline. This family of planes is known as an epipolar pencil. All epipolar lines intersect at the epipole.

Correspondences between images

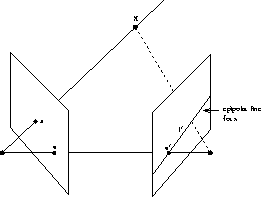
A point in one image generates a line in the other on which its corresponding point must lie. The search for correspondences is thus reduced from a region to a line. This epipolar constraint arises because, for image points corresponding to the same 3D point, the image points, 3D point and optical centres are coplanar.