Application --- Binary Space Partition (BSP)

Three points in 3-space define a plane . The images of these points, together with the epipoles, provide the four correspondences necessary to compute the compatible transformation for . That is, the projective transformation such that

transfers points coplanar with 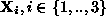. Given it is then possible to distinguish points in 3-space on either side of , using only their image projections and 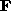i.e. a binary partition of 3-space.

• The three points need not actually correspond to images of physical points, the method can be applied to ``virtual'' planes.

• Points contained in regions of 3-space can be identified using a set of binary space partitions for the planes which bound the region.

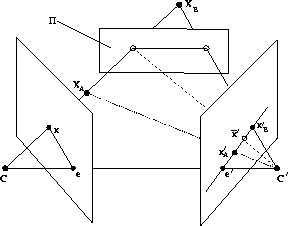
Original images and points

First and second images and corners

BSP 1

Selected planar points, on one side and on the other side

BSP 2

More selected planar points, on one side and on the other side