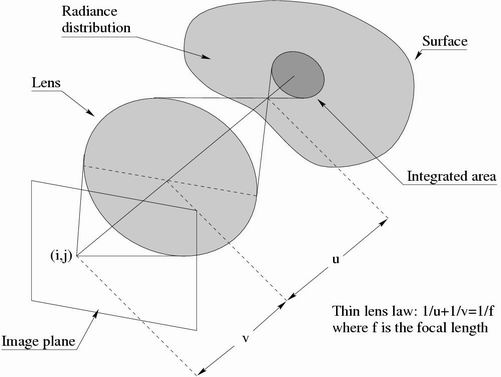
Depth from focus/defocus is the problem of estimating the 3D surface of a scene from a set of two or more images of that scene. The images are obtained by changing the camera parameters (typically the focal setting or the image plane axial position), and taken from the same point of view (see Figure below).

The difference between depth from focus and depth from defocus is that, in the first case it is possible to dynamically change the camera parameters during the surface estimation process, while in the second case this is not allowed(see [1-12] as a sample of the literature on depth from focus/defocus).
In addition, both the problems are called either active or passive depth from focus/defocus, depending on whether it is possible or not to project a structured light onto the scene.
While many computer vision techniques estimate 3D surfaces by using images obtained with pin-hole cameras, in depth from defocus we use real aperture cameras. Real aperture cameras have a short depth of field, resulting in images which appear focused only on a small 3D slice of the scene. The image process formation can be explained with optical geometry. The lens is modeled via the thin lens law, i.e. [ 1/f]=[ 1/v]+[ 1/u], where f is the focal length, u is the distance between the lens plane and the plane in focus in the scene, and v is the distance between the lens plane and the image plane.
A scene is typically modeled as a smooth opaque Lambertian (i.e. with constant bidirectional reflectance distribution function) surface s. Attached to the surface we have a texture r (otherwise called radiance or focused image).
In this case, the intensity I(y) at a pixel y Î Z2 (we denote vector coordinates with boldface fonts) of the CCD surface can be described by:
| (1) |
where the kernel h depends on the surface s and the optical settings u, and x Î R2. For a fixed surface s(x) = d (i.e. a plane parallel to the lens plane at distance d from the lens plane), the kernel h is function of the difference y-x, i.e. integral 1 becomes the convolution
| (2) |
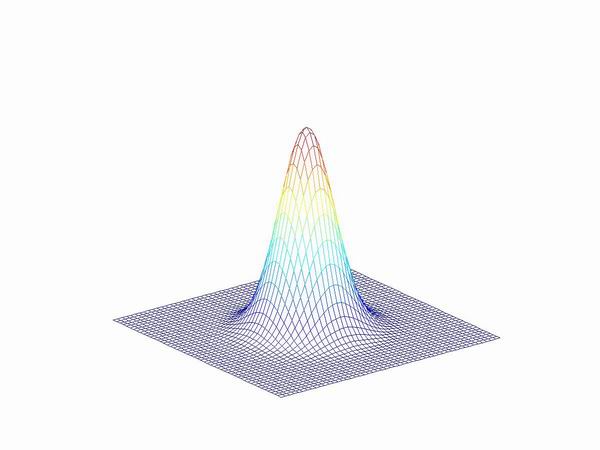
More in general, the kernel h determines the amount of blurring that affects a specific area of the surface in the scene. With ideal optics, the kernel can be represented by a pillbox function. However, in many algorithms for depth from defocus the kernel is approximated by a Gaussian (see Figure below)
| (3) |
Now, the original statement of the problem of depth from defocus can be stated more precisely. Given a set of L ³ 2 images I1...IL obtained with focal settings u1...uL from the same scene, we want to reconstruct the surface s of the scene. For some methods, this may also require to reconstruct the radiance r.
In literature there exists a large variety of approximation models for the above equations. The main exploited simplification is the equifocal assumption. The equifocal assumption consists in representing the surface locally with a plane parallel to the image plane (i.e. an equifocal plane). Then, the image formation process can be locally approximated by Eq. 2.
There also exists a number of real-time systems for depth from defocus. Depth from defocus has been proven to be effective for small distances (e.g. microscopy). Depth from defocus has been compared to stereo vision, provided that the optical system and the scene are properly re-scaled.
Here are some examples of defocused images and the corresponding depth reconstructions.







