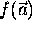G. Taubin (IEEE Trans. PAMI 13(11), pp 1115-1138, Nov 1991) showed that we can approximate the
Euclidean distance to an implicit curve or surface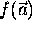 
by its first order
approximation:
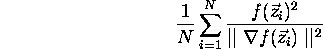
which leads to a generalized eigenvector solution. Let:
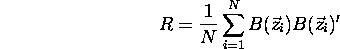
and
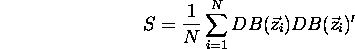
where
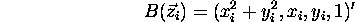
and
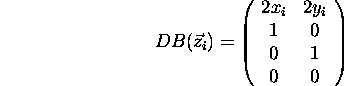
The desired solution is the minimum eigenvalue of the system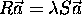 
.
You should have many data points, translate points to surround the origin by subtracting the mean (for numerical stability) and delete data points near the origin (as these are critical points).
Some matlab code for the fit is here and for conversion to standard form is here: