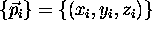Least-square fitting of circles to 3D point data

Bob Fisher

Given a set of N 3D data points 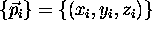we would like to find the 3D circle that best fits these points.

I'm not aware of a direct solution to this problem, so you can do an optimization fit. I don't think it's good enough to find the best 2D circle fit of the points projected onto their best fitting plane, because the projection process loses information.

For an optimization fit, you need a good starting point. You could:

1. pick 3 reasonably separated points and fit a circle to them, or

2. find the plane that best fits the N points, project all points onto the plane and then find the circle best fitting these using the algebraic or approximate Euclidean distance planar circle fit.

With the initial fit, then optimize the parameters to obtain a local minimum of the Euclidean distance over all N points.

6 parameters are needed for the fitting:

3 for the plane that the circle lies in

3 for the circle in that plane

a 2 parameter 3D rotation matrix M that maps planes onto planes,

a 3 parameter 3D circle center

a circle radius .

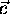
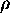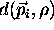as the distance of point 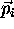from a radius 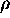circle lying in the XY plane and centered at the origin.

Then you can minimize:

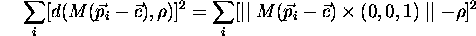
You get the radius 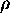and center directly, and the plane that the circle lies in from how M rotates the XY plane.

• About this document ...