III. General Purpose Image Processing
Architectures and Machines
The computer architectures has been classified by Flynn (1966) into four major categories:
· SISD (Single Instruction stream Single Data stream): This is the serial computer architecture.
· MISD (Multiple Instruction stream Single Data stream): This involves several processors, which execute different instructions on the same datum. This category is hypothetical and it is concerned as impractical.
· SIMD (Single Instruction stream Multiple Data stream): Several processors execute the same instruction on different data.
·
MIMD (Multiple Instruction stream
Multiple Data stream): Several processors execute different instructions on
different data.
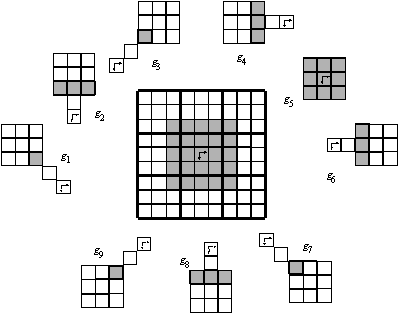
Figure 4. Decomposition of a 9![]() 9-pixel structuring element into 9 3
9-pixel structuring element into 9 3![]() 3-pixel structuring elements.
3-pixel structuring elements.
In image processing, due to the vast amount of data, parallelism is utilized. The parallel architectures can be grouped into two major categories, synchronous and MIMD (Duncan 1990). However this grouping is not unique and overlapping between the categories may be found in the literature (see e.g. (Jonker 1992; Petkov 1993)). According to (Duncan 1990) the categorization is as follows:
· Synchronous
· Vector processors
· SIMD
· Systolic architectures
· MIMD
· Distributed memory
· Shared memory
Vector processors
utilize multiple processing elements coupled on a multiple bus. These elements
are capable of operating both logical and arithmetic operations on either
vector or scalar numbers. The Delft Image Processor (Gerritsen and Aardema
1981; Jonker 1992) (DIP), shown in Fig. 5, can be characterized as a
vector processor. This processor is capable of generating image and
neighborhood points, it can handle floating point numbers and it is able to
perform recursive operations.
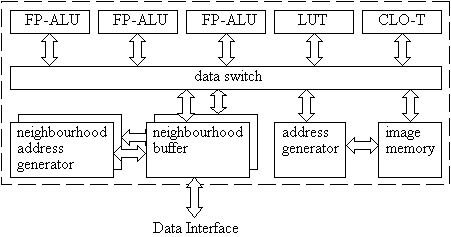
Figure 5. The Delft Image Processor (DIP).
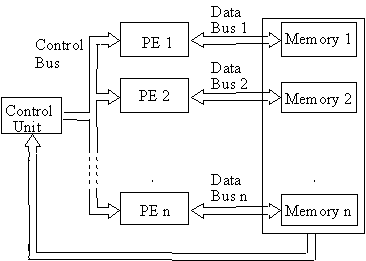
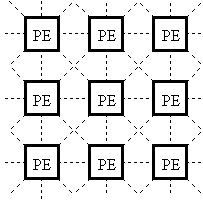
Figure 6. SIMD architecture.
In SIMD
architecture a control unit is used, that provides a single instruction to all
the processing elements concurrently, as shown in Fig. 6. The processing
elements (PEs) execute the instruction on data, which is stored in local
memory. SIMD is the suitable architecture for fast low-level image
processing (Gerritsen and
Aardema 1981; Jonker 1992; Reeves
1984), where mathematical morphology belongs. Examples of
SIMD machines are the CLIP4 (Duff
1982; Preston et al. 1979) the CLIP7A (Fountain
et al. 1988) the AIS-5000 parallel processor (Schmitt and Wilson
1988) and the PAPRICA system (Broggi et al. 1998; Broggi et al.
1997). The processing element of CLIP4 and its network
topology are shown in Figs. 7a and 7b, respectively. As it is shown in this
figure each processing element communicates with its eight nearest neighbors.
For cellular logic operations the neighborhood can be accessed in parallel, as
it happens in all the architectures based on cellular automata. However it is
possible to perform recursive neighborhood operations, as well, via feedback
obtained by the carry flip-flop. The CLIP7 chip is a successor of CLIP4. This
is supplied with more memory per processor, improved image I/O speeds,
increased local control and multi-bit structure.
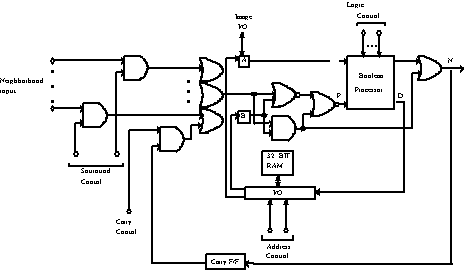
(a)
(b)
Figure 7.The CLIP4 image processor: (a) block diagram of the processing element and (b) network topology.
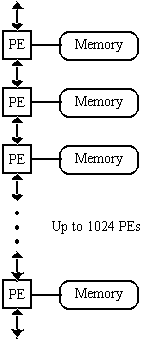
The AIS-5000
system consists of an SIMD array parallel processor, a general-purpose
microprocessor and high-speed I/O hardware for the parallel processor. The
parallel array can contain up to 1024 programmable PEs with local memory and
connections with two neighbors PEs, as shown in Fig. 8a. The PEs are
programmable and can perform several operations, such as Boolean, arithmetic
and neighborhood operations. The implementation of such a neighborhood
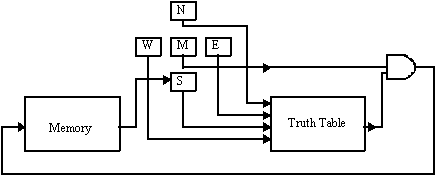
operation, named erode_nbr, is shown in Fig. 8b. The PE is programmed via the
truth table, which is given in hexadecimal number. An example of a truth table,
the corresponding hexadecimal number and the structuring element are provided
in Fig. 8c.
(a)
(b)

(c)
Figure 8. (a) The AIS-5000 parallel array topology and (b) implementation of binary erosion on the AIS-5000 system (c) a structuring element and the corresponding truth table for binary erosion.
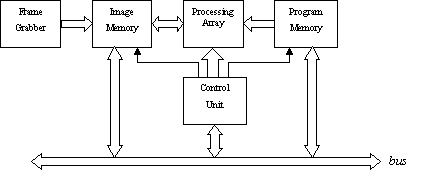
The PAPRICA system
has been designed and realized as a massively parallel morphological
coprocessor. It based on a hierarchical morphological computational model.
PAPRICA was designed to be attached on general-purpose machines. It comprises
five major functional parts (Fig. 9a). These are the frame grabber (grabs 512![]() 512 images with 8 bit/pixel resolution at video
rate), the program memory, the image memory, the processor array and the
control unit. The main part ofPAPRICA system is its processor array in which
fits exactly the input image. This array consists of two different type
internal registers: the morphological registers (MOR) and the logical register
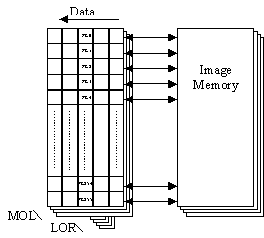
(LOR), as shown in Fig. 9b (PAPRICA-3 version with 256 PEs). The MOR consist of
5-bit shift-registers, which allow to perform morphological operations on an
enhanced 3
512 images with 8 bit/pixel resolution at video
rate), the program memory, the image memory, the processor array and the
control unit. The main part ofPAPRICA system is its processor array in which
fits exactly the input image. This array consists of two different type
internal registers: the morphological registers (MOR) and the logical register
(LOR), as shown in Fig. 9b (PAPRICA-3 version with 256 PEs). The MOR consist of
5-bit shift-registers, which allow to perform morphological operations on an
enhanced 3![]() 3, cross-like, neighborhood as the one shown in Fig.
9c. The LOR are used to perform temporary storage, as well as for temporary
storage.
3, cross-like, neighborhood as the one shown in Fig.
9c. The LOR are used to perform temporary storage, as well as for temporary
storage.
(a)
(b)

(c)
Figure 9. (a) Block diagram of the PAPRICA system, (b)
the PE topology of PAPRICA-3 and (c) the enhanced 3![]() 3neighborhood.
3neighborhood.
Systolic
architectures or systolic arrays are the most widely used architectures for
low-level image processing. A systolic array is designed to embody a certain
algorithm in hardware. The PEs of a systolic architecture are rigid, i.e. they
are not programmable. The data is pipelined in rhythmic fashion from the memory
to the network of the PEs and it returns back to the memory. The network
topology of a systolic array, denoting the data flow path is shown in Fig. 10.
The synchronization of data is achieved through a global clock, which controls
all the PEs. Implementations of systolic arrays for morphological image
processing are analytically described in the next section.
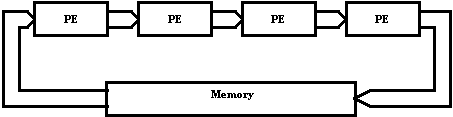
Figure 10.Systolic array network topology and data flow path.
The MIMD
architectures are discriminated into distributed-memory architectures (ring,
mesh, pyramid, hypercube) and shared-memory architectures (Hwang and Briggs
1987). The distributed memory architectures consist of
several processors interconnected in various ways. Each processor communicates
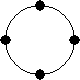
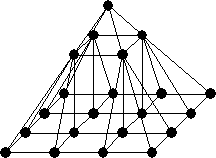
with its local memory as well as with the adjacent processors. Fig. 11a depicts
the ring topology architecture. This topology is appropriate for a limited
number of nodes and it is suitable for algorithms, which do not demand vast
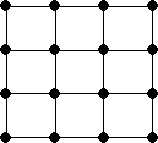
data exchange. A more sophisticated topology is the mesh topology (Rosenfeld
1983), shown in Fig. 11b. This can be applied into
algorithms involved with matrixes, such as 2-D image processing. However, many
low and intermediate level image processing algorithms require comparison of
pixels which are distant located; in this topology the communication between
two nodes not belonging in the same neighbor is slow. An extension of the mesh
topology is the pyramid topology. This consists of overlapping meshes with
successively lower resolution, as shown in Fig. 11c.
(a) (b) (c)
Figure 11.Distributed-memory network topologies: (a) ring, (b) mesh and (c) pyramid.
The pyramid
topology is suitable for the implementation of low and intermediate level image
processing; especially those that are dominated by data transaction between
spatial distance pixels. Another more complicated topology is the hypercube
topology (Frieder
1990). According to this architecture the nodes are located
on the corners of an n dimension cube. A machine of dimension d,
built on this architecture, has 2d nodes, each being
connected to its d neighbor nodes. Figs. 12a, 12b, 12c and 12d depict
the topology of a one-dimensional (1-D), a two-dimensional (2-D), a
three-dimensional (3-D) and a four-dimensional (4-D) hypercube respectively. A
paradigm of a hypercube structure `(enhanced hypercube) for machine vision
applications is Proteus (Haralick
et al. 1995). The topology of Proteus architecture is shown in
Fig. 13. It is a hierarchical re-configurable interconnection network with its
highest level being a circuit switched enhanced hypercube. The Proteus system
is capable of performing morphological image processing tasks such as dilation,
erosion, closing and opening. It accepts the data via multiple links at a rate
up to 640MBps.
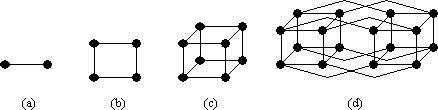
Figure 12. Hypercube network topologies: (a) 1-D, (b)
2-D, (c) 3-D and (d) 4-D.
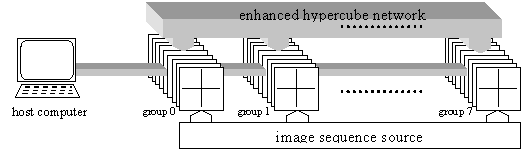
Figure 13. The Proteus enhanced hypercube topology.
In shared memory
architectures the PEs are controlled by a common memory. Generally speaking
there are two ways of interfacing the PEs with memory. The simple one consists
of a fast bus on which the PEs and the memory are tied Fig. 14a. Such machines
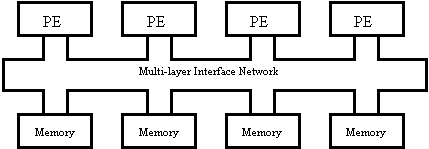
typically consist of up to 30 PEs. The more sophisticated way comprises a
multi-layer interface network, which is responsible to interconnect the PEs
with the pieces of memory Fig. 14b. The main advantage of the machines built on
with shared memory architecture is that they are easily implemented. These
machines though are rather used in high-level, than in low-level image
processing. Although such machines are applicable to parallel image processing,
where each PE is devoted to a certain particle of the image, they are not as
sufficient as SIMD. Due to the synchronization that should be applied on the
PEs, the system becomes time-consuming. However, many structures adopt cash
memory in each PE, in order to enhance their speed.
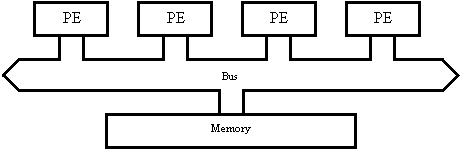
(a)
(b)
Figure 14.Shared memory architectures: (a) fast bus and (b) multi-layer interface network.
Duncan R (1990) A Survey of Parallel Computer Architectures, IEEE Computer, 23: 5-16.
Flynn M J (1966) Very High Speed Computing Systems, Proceedings of the IEEE, 56 (12): 1901-1909.
Haralick R M and Shapiro L G (1992): Computer and Robot Vision, Addison-Wesley, New York.
Klein J C and Serra J (1977) The Texture Analyzer, Journal of Microscopy, 95: 349-356.
Mano M M (1991): Digital Design, Prentice-Hall, Englewood Cliffs, NJ.
Petkov N (1993): Systolic Parallel Processing, North-Holland, Amsterdam, The Netherlands.
Rosenfeld A (1983) Parallel Image Processing Using Cellular Arrays, IEEE Computer, 16: 14-20.
Serra J (1982): Image Analysis and Mathematical Morphology, Academic Press, London.
Zhuang X and Haralick R M (1986) Morphological Structuring Element Decomposition,
Computer Vision, Graphics and Image Processing, 35 (3): 370-382.