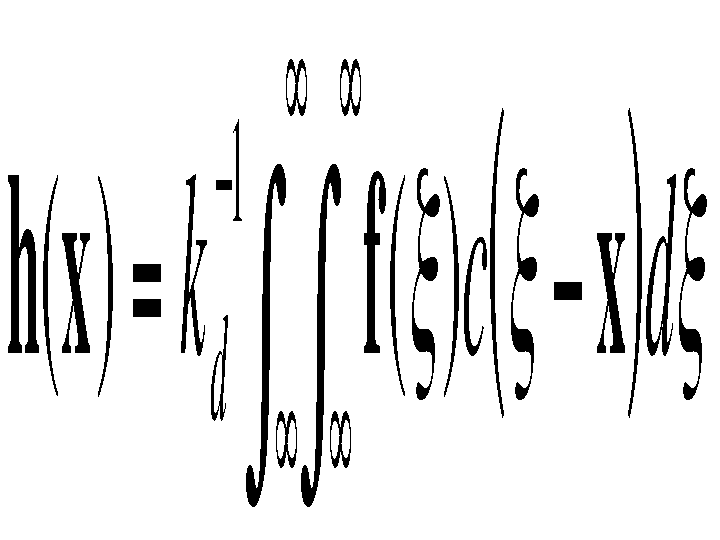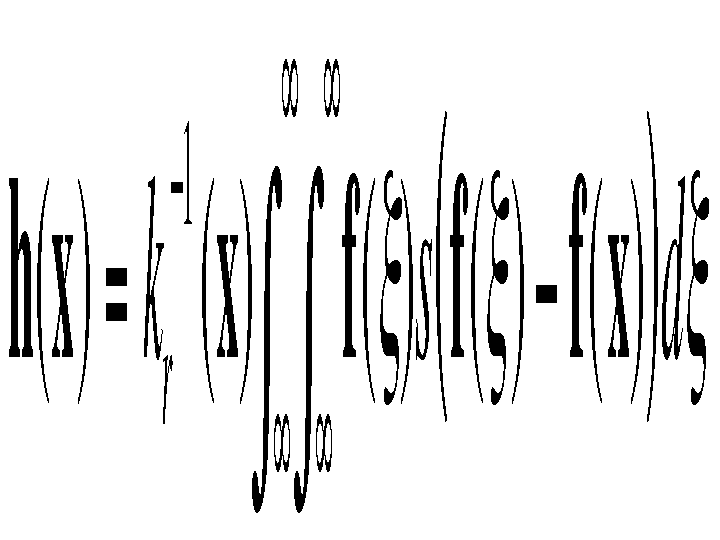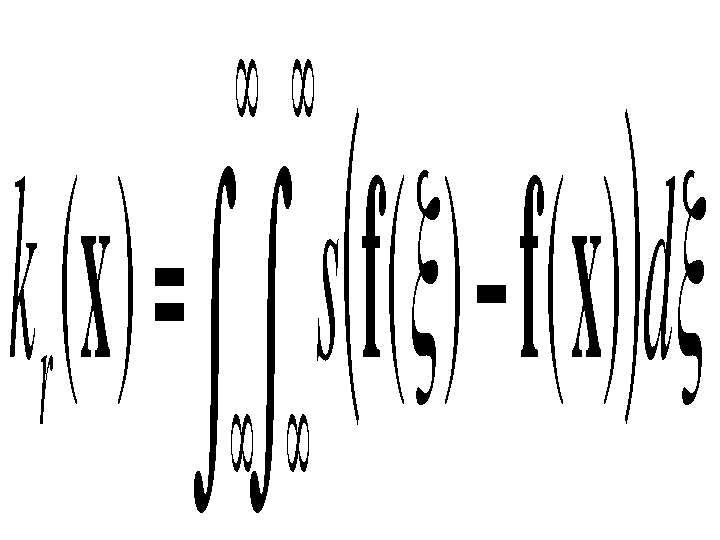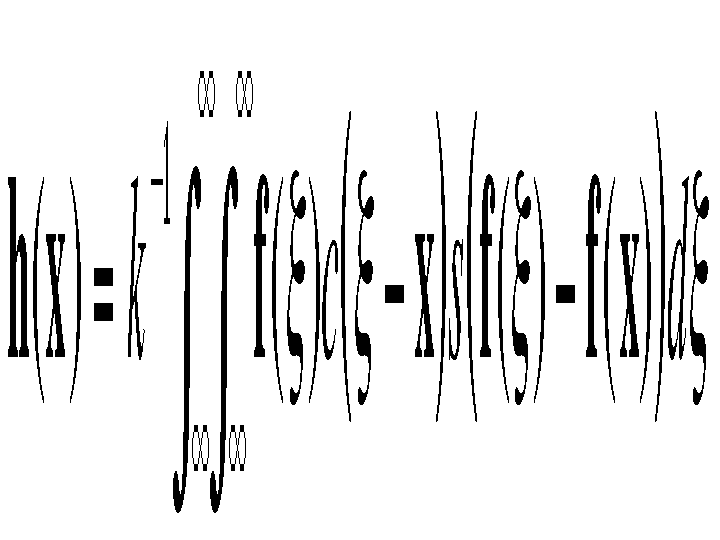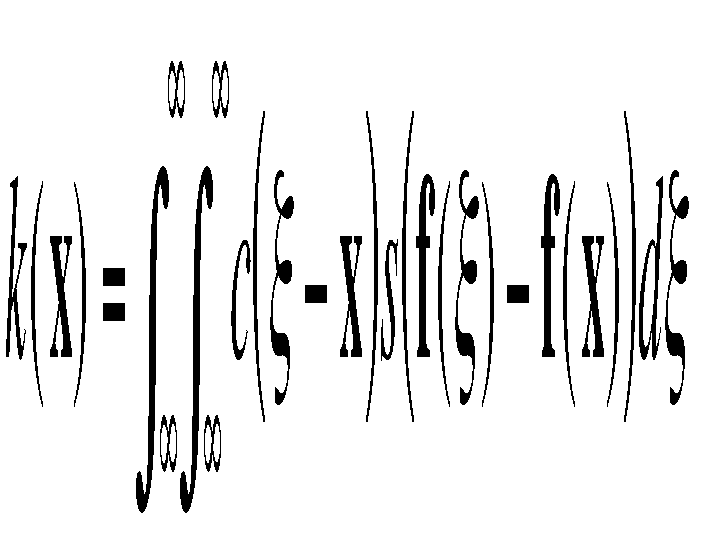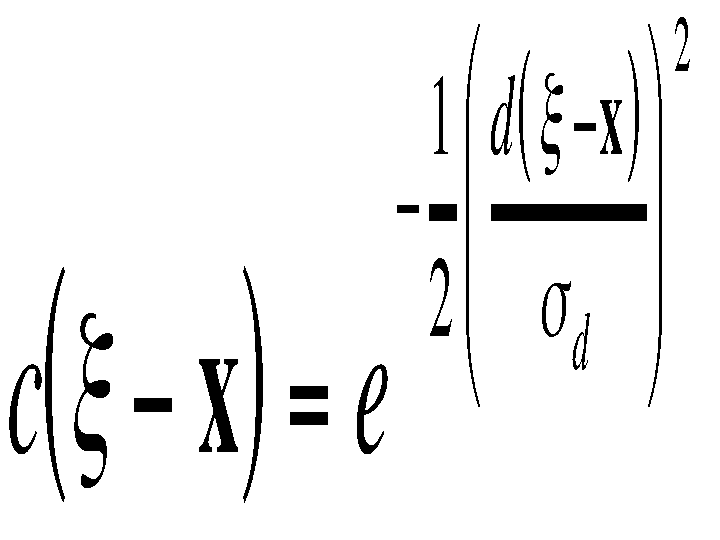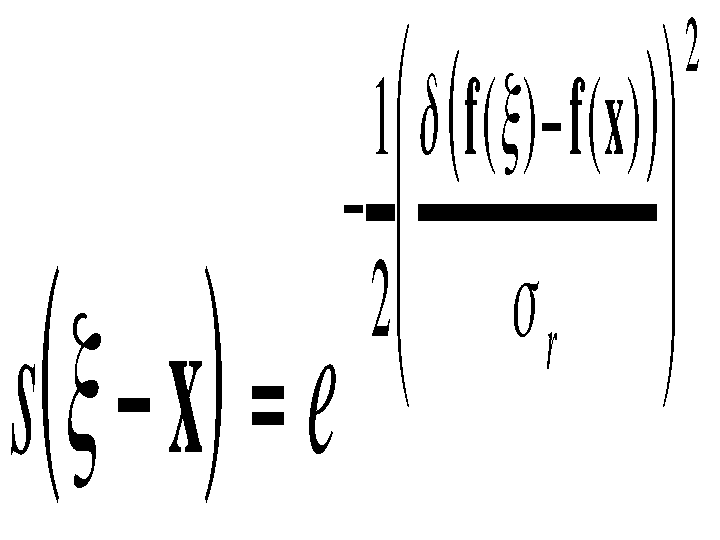Bilateral Filtering for Gray and
Color Images
- Introduction
- The
Idea
- The Gaussian
Case
- Experiments with
Black-and-White Images
- Experiments with Color
Images
- References
Introduction
Filtering is perhaps the most fundamental
operation of image processing and computer vision. In the broadest
sense of the term "filtering", the value of the filtered image at a
given location is a function of the values of the input image in a
small neighborhood of the same location. For example, Gaussian
low-pass filtering computes a weighted average of pixel values in the
neighborhood, in which the weights decrease with distance from the
neighborhood center. Although formal and quantitative explanations of
this weight fall-off can be given, the intuition is that images
typically vary slowly over space, so near pixels are likely to have
similar values, and it is therefore appropriate to average them
together. The noise values that corrupt these nearby pixels are
mutually less correlated than the signal values, so noise is averaged
away while signal is preserved.
The assumption of slow spatial variations fails at edges, which are
consequently blurred by linear low-pass filtering. How can we prevent
averaging across edges, while still averaging within smooth regions?
Many
efforts have been devoted to reducing this
undesired effect. Bilateral
filtering is a simple, non-iterative
scheme for edge-preserving
smoothing.
Back to Index
The Idea
The basic idea underlying bilateral filtering is
to do in the range of an image what traditional filters do in its
domain. Two pixels can be close to one another, that is,
occupy nearby spatial location, or they can be similar to one another, that is,
have nearby values, possibly in a perceptually meaningful
fashion.
Consider a shift-invariant low-pass domain filter applied to an
image:
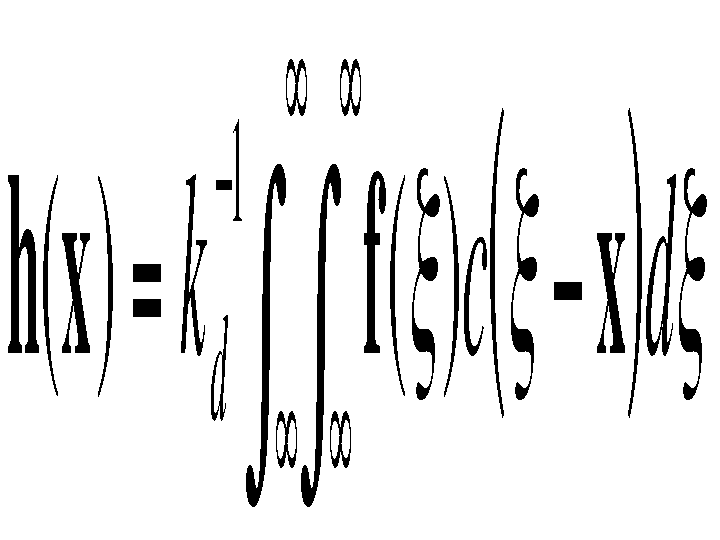
The bold font for f and h
emphasizes the fact that both input and output images may be
multi-band. In order to preserve the DC component, it must be
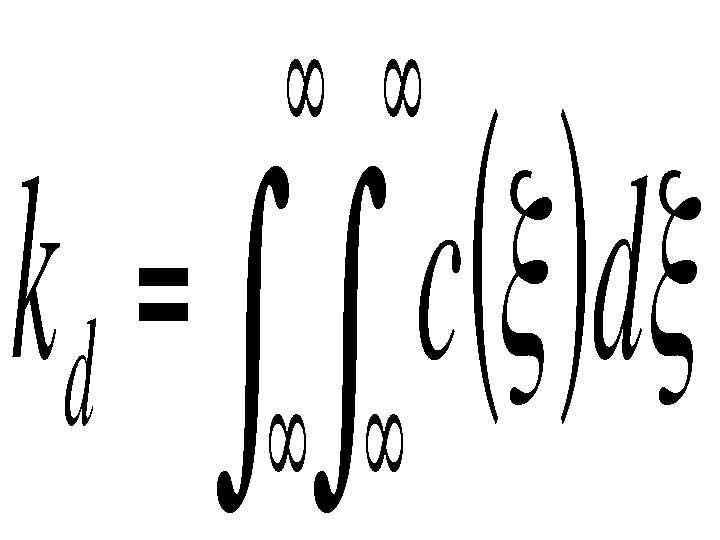
Range filtering is similarly defined:
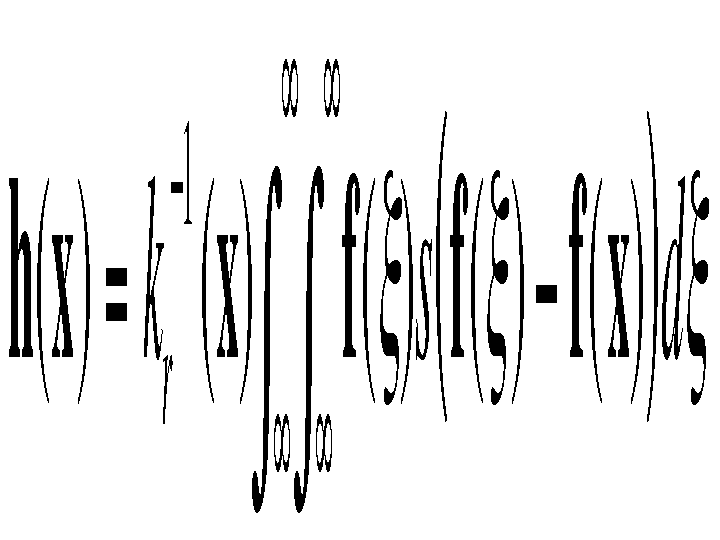
In this case, the kernel measures the photometric similarity between
pixels. The normalization constant in this case is
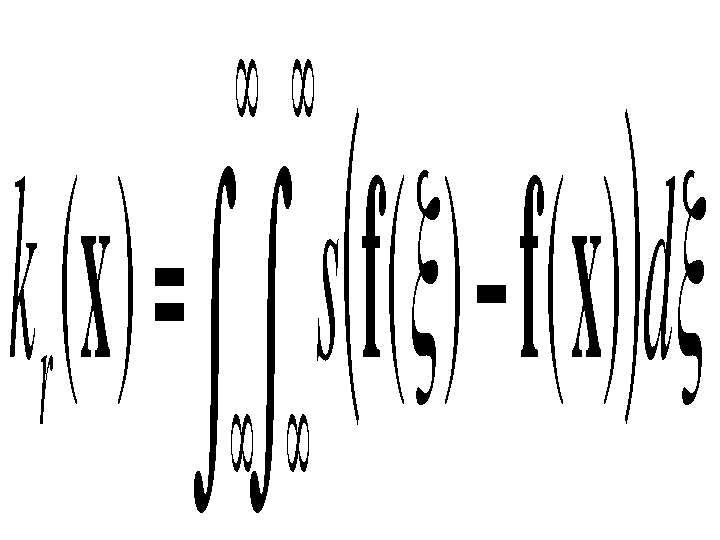
The spatial distribution of image intensities plays no role in range
filtering taken by itself. Combining intensities from the entire
image, however, makes little sense, since the distribution of image
values far away from x ought not to affect the final value at x. In addition, one can show
that range filtering without domain filtering merely changes the
color map of an image, and is therefore of little use. The
appropriate solution is to combine domain and range filtering,
thereby enforcing both geometric and photometric locality. Combined
filtering can be described as follows:
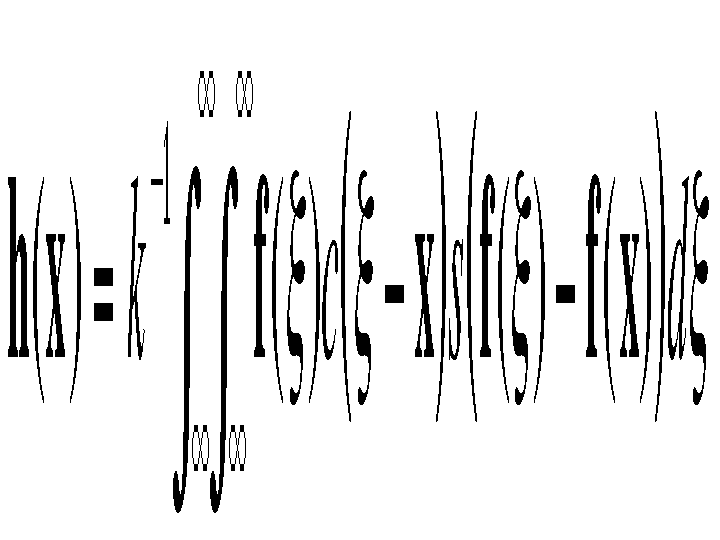
with the normalization
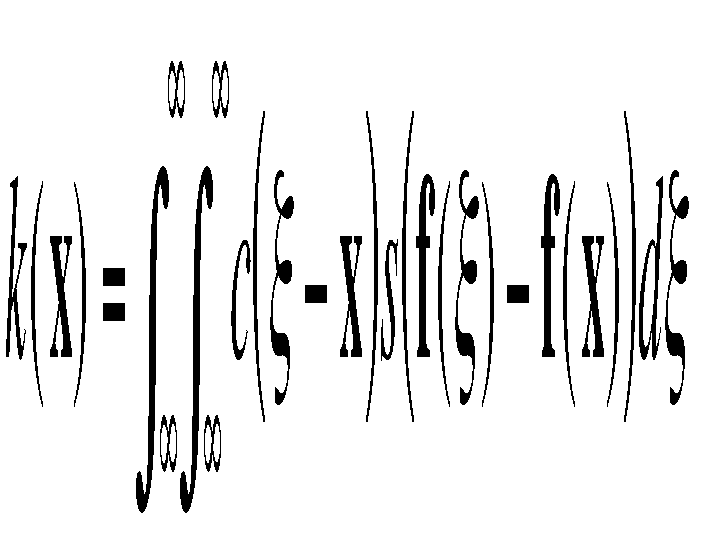
Combined domain and range filtering will be denoted as
bilateral filtering. It replaces the pixel value at x with an average of similar and
nearby pixel values. In smooth regions, pixel values in a small
neighborhood are similar to each other, and the bilateral filter acts
essentially as a standard domain filter, averaging away the small,
weakly correlated differences between pixel values caused by noise.
Consider now a sharp boundary between a dark and a bright region, as
in figure 1(a).
When the bilateral filter is centered, say, on a pixel on the bright
side of the boundary, the similarity function s assumes values close to one
for pixels on the same side, and values close to zero for pixels on
the dark side. The similarity function is shown in figure 1(b) for a
23x23 filter support centered two pixels to the right of the step in
figure 1(a). The normalization term k(x) ensures that the weights for
all the pixels add up to one. As a result, the filter replaces the
bright pixel at the center by an average of the bright pixels in its
vicinity, and essentially ignores the dark pixels. Conversely, when
the filter is centered on a dark pixel, the bright pixels are ignored
instead. Thus, as shown in figure 1(c), good filtering behavior is
achieved at the boundaries, thanks to the domain component of the
filter, and crisp edges are preserved at the same time, thanks to the
range component.
Back to Index
The Gaussian
Case
A simple and important case of bilateral filtering
is shift-invariant Gaussian filtering, in which both the closeness
function c and
the similarity function s are Gaussian functions of the Euclidean distance between
their arguments. More specifically, c is radially symmetric:
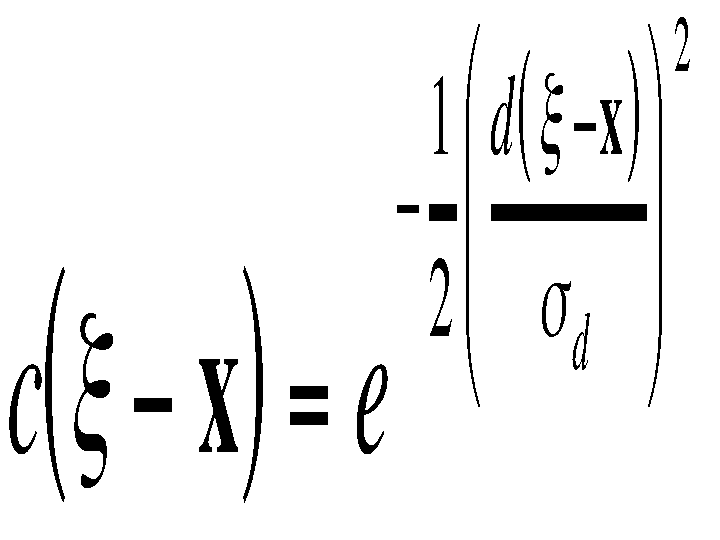
where
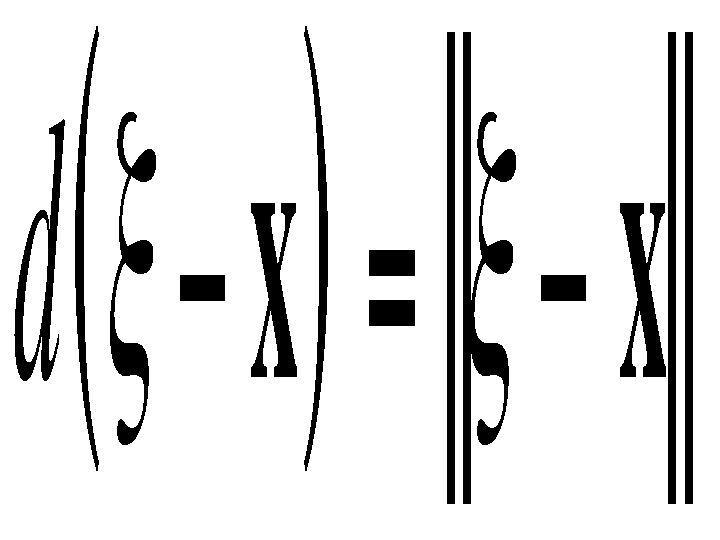
is the Euclidean distance. The similarity function s is perfectly analogous to
c :
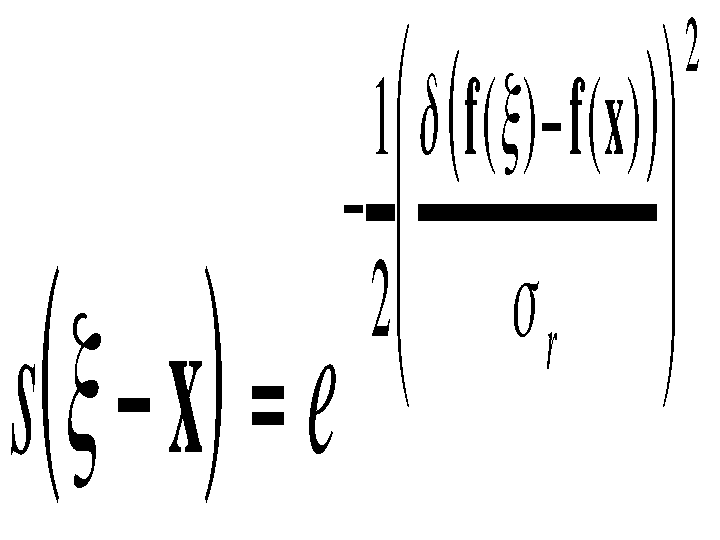
where
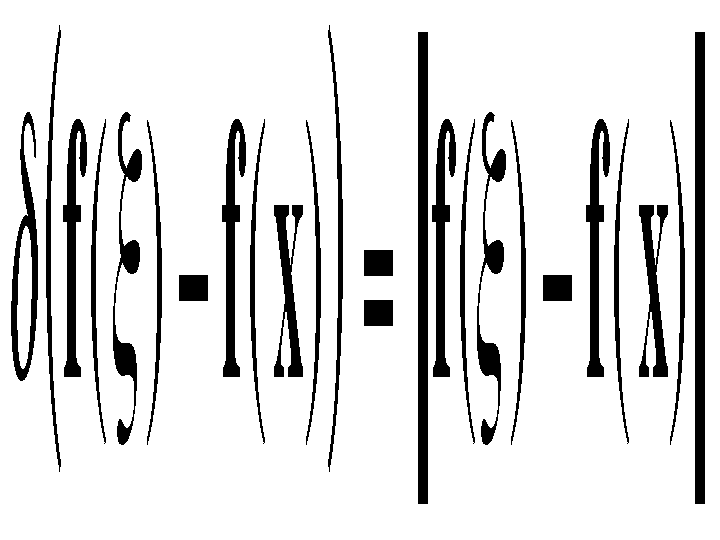
is a suitable measure of distance in intensity space. In the scalar
case, this may be simply the absolute difference of the pixel
difference or, since noise increases with image intensity, an
intensity-dependent version of it. Just as this form of domain
filtering is shift-invariant, the Gaussian range filter introduced
above is insensitive to overall additive changes of image intensity.
Of course, the range filter is shift-invariant as well.
Back to Index
Experiments with
Black-and-White Images
Figure 2 (a) and (b) show the potential of
bilateral filtering for the removal of texture. The picture
"simplification" illustrated by figure 2 (b) can be useful for data
reduction without loss of overall shape features in applications such
as image transmission, picture editing and manipulation, image
description for retrieval.
|

|
|

|
|
(a)
|
|
(b)
|
|
|
Figure 2
|
|
Bilateral filtering with parameters sd =3 pixels and
sr =50
intensity values is applied to the image in figure 3 (a) to yield the
image in figure 3 (b). Notice that most of the fine texture has been
filtered away, and yet all contours are as crisp as in the original
image. Figure 3 (c) shows a detail of figure 3 (a), and figure 3 (d)
shows the corresponding filtered version. The two onions have assumed
a graphics-like appearance, and the fine texture has gone. However,
the overall shading is preserved, because it is well within the band
of the domain filter and is almost unaffected by the range filter.
Also, the boundaries of the onions are preserved.
Back to Index
Experiments with Color
Images
For black-and-white images, intensities between
any two gray levels are still gray levels. As a consequence, when
smoothing black-and-white images with a standard low-pass filter,
intermediate levels of gray are produced across edges, thereby
producing blurred images. With color images, an additional
complication arises from the fact that between any two colors there
are other, often rather different colors. For instance, between blue
and red there are various shades of pink and purple. Thus, disturbing
color bands may be produced when smoothing across color edges. The
smoothed image does not just look blurred, it also exhibits
odd-looking, colored auras around objects.
Figure 4 (a) shows a detail from a picture with a red jacket against
a blue sky. Even in this unblurred picture, a thin pink-purple line
is visible, and is caused by a combination of lens blurring and pixel
averaging. In fact, pixels along the boundary, when projected back
into the scene, intersect both red jacket and blue sky, and the
resulting color is the pink average of red and blue. When smoothing,
this effect is emphasized, as the broad, blurred pink-purple area in
figure 4 (b) shows.
To address this difficulty, edge-preserving smoothing could be
applied to the red, green, and blue components of the image
separately. However, the intensity profiles across the edge in the
three color bands are in general different. Smoothing the three color
bands separately results in an even more pronounced pink and purple
band than in the original, as shown in figure 4 (c). The pink-purple
band, however, is not widened as in the standard-blurred version of
figure 4 (b).
A much better result can be obtained with bilateral filtering. In
fact, a bilateral filter allows combining the three color bands
appropriately, and measuring photometric distances between pixels in
the combined space. Moreover, this combined distance can be made to
correspond closely to perceived dissimilarity by using Euclidean
distance in the CIE-Lab color
space. This color space is based on a
large body of psychophysical data concerning color-matching
experiments performed by human observers. In this space, small
Euclidean distances are designed to correlate strongly with the
perception of color discrepancy as experienced by an "average"
color-normal human observer. Thus, in a sense, bilateral filtering
performed in the CIE-Lab color space is the most natural type of
filtering for color images: only perceptually similar colors are
averaged together, and only perceptually important edges are
preserved. Figure 4 (d) shows the image resulting from bilateral
smoothing of the image in figure 4 (a). The pink band has shrunk
considerably, and no extraneous colors appear.
Figure 5 (c) shows the result of five iterations of bilateral
filtering of the image in figure 5 (a). While a single iteration
produces a much cleaner image (figure 5 (b)) than the original, and
is probably sufficient for most image processing needs, multiple
iterations have the effect of flattening the colors in an image
considerably, but without blurring edges. The resulting image has a
much smaller color map, and the effects of bilateral filtering are
easier to see when displayed on a printed page. Notice the
cartoon-like appearance of figure 5 (c). All shadows and edges are
preserved, but most of the shading is gone, and no "new" colors are
introduced by filtering.
Back to Index
References
[1] C. Tomasi and R. Manduchi,
"Bilateral Filtering for Gray and Color Images", Proceedings of the 1998 IEEE International Conference on
Computer Vision, Bombay, India.
[2] T. Boult, R.A. Melter, F. Skorina, and I.
Stojmenovic,"G-neighbors", Proceedings of
the SPIE Conference on Vision Geometry II,
pages 96-109, 1993.
[3] R.T. Chin and C.L. Yeh, "Quantitative evaluation of some
edge-preserving noise-smoothing techniques", Computer Vision, Graphics, and Image
Processing, 23:67-91, 1983.
[4] L.S. Davis and A. Rosenfeld, "Noise cleaning by iterated local
averaging", IEEE Transactions on Systems,
Man, and Cybernetics, 8:705-710, 1978.
[5] R.E. Graham, "Snow-removal - a noise-stripping process for
picture signals", IRE Transactions on
Information Theory, 8:129-144, 1961.
[6] N. Himayat and S.A. Kassam, "Approximate performance analysis of
edge preserving filters", IEEE Transactions
on Signal Processing, 41(9):2764-77,
1993.
[7] T.S. Huang, G.J. Yang, and G.Y. Tang, "A fast two-dimensional
median filtering algorithm", IEEE
Transactions on Acoustics, Speech, and Signal
Processing, 27(1):13-18, 1979.
[8] J.S. Lee, "Digital image enhancement and noise filtering by use
of local statistics", IEEE Transactions on
Pattern Analysis and Machine Intelligence,
2(2):165-168, 1980.
[9] M. Nagao and T. Matsuyama, "Edge preserving smoothing",
Computer Graphics and Image
Processing, 9:394-407, 1979.
[10] P.M. Narendra, "A separable median filter for image noise
smoothing", IEEE Transactions on Pattern
Analysis and Machine Intelligence,
3(1):20-29, 1981.
[11] K.J. Overton and T.E. Weymouth, "A noise reducing preprocessing
algorithm",Proceedings of the IEEE Computer
Science Conference on Pattern Recognition and Image
Processing, pages 498-507, Chicago, IL,
1979.
[12] P. Perona and J. Malik, "Scale-space and edge detection using
anisotropic diffusion", IEEE Transactions
on Pattern Analysis and Machine Intelligence, 12(7):629-639, 1990.
[13] G. Ramponi, "A rational edge-preserving smoother",
Proceedings of the International Conference
on Image Processing, volume 1, pages
151-154, Washington, DC, 1995.
[14] G. Sapiro and D.L. Ringach, "Anisotropic diffusion of color
images", Proceedings of the
SPIE, volume 2657, pages 471-382,
1996.
[15] D.C.C. Wang, A.H. Vagnucci, and C.C. Li, "A gradient inverse
weighted smoothing scheme and the evaluation of its performance",
Computer Vision, Graphics, and Image
Processing, 15:167-181, 1981.
[16] G. Wyszecki and W. S. Styles, Color Science: Concepts and Methods, Quantitative Data and
Formulae, John Wiley and Sons, New York,
NY, 1982.
[17] L. Yin, R. Yang, M. Gabbouj, and Y. Neuvo, "Weighted median
filters: a tutorial",IEEE Transactions on
Circuits and Systems II: Analog and Digital Signal
Processing, 43(3):155-192, 1996.