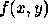 .
.


Digitised images are an approximate representation of the real world. As mentioned previously, they are subject to sampling,
quantisation, windowing and noise. Normally, they are represented in a two dimensional spatial domain,
i.e. x and y, or 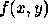 .
.
However, they may equally be represented in a spatial frequency
domain, 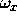 and
and  . Transformation from one domain
to another is based commonly on Fourier analysis. Usually, this
is devloped in one dimension for example, in the analysis of
speech or music where
. Transformation from one domain
to another is based commonly on Fourier analysis. Usually, this
is devloped in one dimension for example, in the analysis of
speech or music where 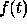 is a time varying signal; here we consider
briefly the extension to two dimensions.
is a time varying signal; here we consider
briefly the extension to two dimensions.
Image transforms are widely used in filtering, data compression, image description, e.g. extraction of frequency domain characteristics for classification of texture, image restoration and low level processing. Low level image processing operations transform generally from one image to another image; this might be the first stage in a computer vision system. Considering first the equivalence of the time and frequency domains, this can be described by the Fourier transformation, where
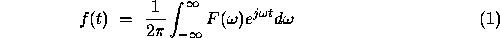
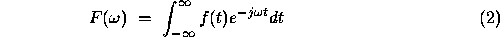
Figure 1: Examples of one dimensional signals and their corresponding transforms
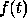 and
and 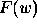 are continuous aperiodic signals of
time, t, and radial frequency,
are continuous aperiodic signals of
time, t, and radial frequency, 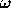 , respectively.
In image processing terms, transformation between the spatial
, respectively.
In image processing terms, transformation between the spatial
 and spatial frequency
and spatial frequency 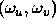 domains is expressed,
domains is expressed,

and
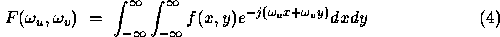
where  describes the intensity function of an image
and
describes the intensity function of an image
and 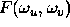 is it's
frequency spectrum in terms of the variables
is it's
frequency spectrum in terms of the variables  , which corresponds to
a frequency variable along the x-axis
and
, which corresponds to
a frequency variable along the x-axis
and 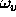 , which corresponds to a
frequency variable along the y-axis.
In a digitised image, the incoming signal is sampled at discrete
intervals in space. Assuming a square image of dimension, N,
the corresponding transformational equations are,
, which corresponds to a
frequency variable along the y-axis.
In a digitised image, the incoming signal is sampled at discrete
intervals in space. Assuming a square image of dimension, N,
the corresponding transformational equations are,

and

The 2-dimensional Fourier transform of an digital image is thus
essentially a Fourier series representation of a 2-dimensional field.
Within a digital image processing system, the computation of these equations
requires 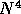 operations but this can be reduced substantially
by successive passes of the 1-dimensional FFT to
operations but this can be reduced substantially
by successive passes of the 1-dimensional FFT to 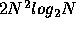 .
.

[ Quantisation, Sampling and Noise ]

Comments to: Sarah Price at ICBL.
(Last update: 4th July, 1996)