To apply the technique of feature space transformation, the sought after curves must be of known form, expressed either parametrically or as a stored general shape. In the simplest case, a single transformation is applied to all feature points mapping them into parameter space. The transformation is found by inverting the parametric characterisation of the boundary sought, then finding the parameters as a function of the feature point values.
The simplest application of this procedure is the Hough transformation to detect straight lines. A straight line may be expressed as
in which the feature (image) space is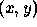 
and the parameter space is 
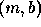defining the gradient and intercept of the line respectively. This parameterisation is inconvenient since both m and b can assume a value of infinity, so that the normal parameterisation of the straight line is more commonly used, as illustrated in Figure 2, below.
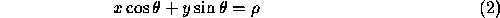
where defines the angle which the normal of length makes with the x-axis.
Each straight line is uniquely defined by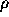 
and 
, and 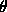for every point 
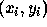in the original image it is possible to create a mapping
from feature to transformational space. If the angle of the edge data is known, a one-to-one mapping is possible, as illustrated in Figure 2, below.
but if this is unknown then a one-to-many mapping is required, according to the quantised values of the possible angle. In this case, the mapping is from a point in image space to a sine wave in transformational space.The process is repeated for all edge points in the feature space until a two-dimensional accumulator array is formed having quantised values for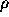 
and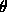 
. The quantisation values should be chosen to be compatible with the expected
accuracy of the edge detection process. In order to detect the presence of a given straight line in the boundary data it is necessary to detect peaks in the transformational space.
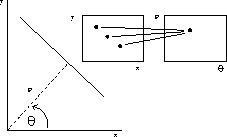
Figure 2: Transformation from image to Hough space
space. Hence it is necessary to record the position of the points 
which gave rise to them, and/or to re-examine the edge data along the predicted lines to assess the true line position.
This general principle may be extended to higher order features, at the expense of greater complexity of computation. For example, it is possible to detect a parabola of form
or a circle of form
In general terms, an arbitrary curve is represented by an equation
where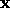 
is the image space vector, in this case 
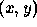and
is the parameter vecor,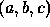 
for the parabola, and
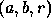for the circle. The general algorithm is
Quantise parameter space within limits of. For a three parameter vector the parameter space is three dimensional. Set all elements of quantised parameter space to zero. For each image point
in the thresholded image, increase all elements of parameter space where
. Detect local maxima in the parameter space
Considering the parabola as an example, for a given point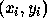 
there are clearly several variations of the parameters 
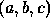which satisfy 
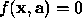. In effect, this becomes
For each possible value of a For each possible value of b Compute the value of the c parameter
but this can be reduced in complexity if the edge direction is known, since differentiating equation 3
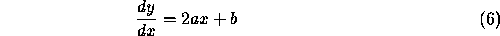
For each possible value of a Compute the value of b from equation 6 Compute the value of c from equation 3
An example of Hough transformation is shown below. the original image includes some old and new coins viewed against a grid; a new 20p is not truly circular. The algorithm detects lines and circles in Hough space then back-projects the predictions onto the image space and checks the extent of the segment data. There are several heuristics, the edge threshold, the peak threshold in Hough space, and the strength and angular tolerance allowed when comparing the back projected lines to the image data.
Comments to: Sarah Price at ICBL.
(Last update: 22th April, 1996)
