 Splitting
Splitting
and Merging

Splitting and merging attempts to divide an image into uniform regions. The basic representational structure is pyramidal, i.e. a square region
of size m by m at one level of a pyramid has 4 sub-regions of size 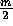 by
by 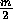 below it in the pyramid. Usually the algorithm starts from the initial assumption that the entire image is a single region, then computes the homogeneity criterion to see if it is TRUE. If FALSE, then the square region is split into the four smaller regions. This process is then repeated on each of the sub-regions until no further splitting is necessary. These small square regions are then merged if they are similar to give larger irregular regions. The problem (at least from a programming point of view) is that any two regions may be merged if adjacent and if the larger region satisfies the homogeneity criteria, but regions which are adjacent in image space may have different parents or be at different levels (i.e. different in size) in the pyramidal structure. The process terminates when no further merges are possible.
below it in the pyramid. Usually the algorithm starts from the initial assumption that the entire image is a single region, then computes the homogeneity criterion to see if it is TRUE. If FALSE, then the square region is split into the four smaller regions. This process is then repeated on each of the sub-regions until no further splitting is necessary. These small square regions are then merged if they are similar to give larger irregular regions. The problem (at least from a programming point of view) is that any two regions may be merged if adjacent and if the larger region satisfies the homogeneity criteria, but regions which are adjacent in image space may have different parents or be at different levels (i.e. different in size) in the pyramidal structure. The process terminates when no further merges are possible.
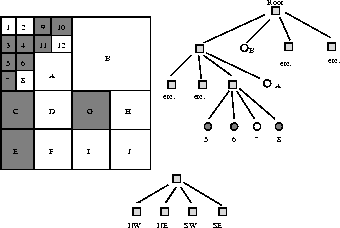
Figure 1: Quad splitting of an image
Although it is common to start with the single region assumption, it is possible to start at an intermediate level, e.g. 16 regions or whatever.
In the latter case, it is possible that 4 regions may be merged to form a parent region. For simplicity, assume we start with a single region, i.e. the whole image. Then, the process of splitting is simple. A list of current regions to be processed, i.e. regions
defined as not homogeneous is maintained. When a region is found to be homogeneous it is removed from the ProcessList and placed on a RegionList.
Algorithm for successive region splitting
Set ProcessList = IMAGE
Repeat
Extract the first element of ProcessList
If the region is uniform then add to RegionList
Else split the region into 4 sub-regions and add these to ProcessList
Until ( all regions removed from ProcessList)
Uniformity is determined on the basis of homogeneity of property as in the previous examples. For a grey level image, say, a region is said to be statistically homogeneous if the standard deviation of the intensity less than some threshold value, where the standard deviation is given by,
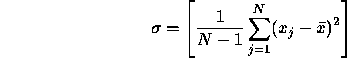
and 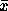 is the mean intensity of the N pixels in the region.
Whereas splitting is quite simple, merging is more complex. Different algorithms are possible, some use the same test for homogeneity but others use the difference in average values. Generally, pairs of regions are compared, allowing more complex shapes to emerge.
is the mean intensity of the N pixels in the region.
Whereas splitting is quite simple, merging is more complex. Different algorithms are possible, some use the same test for homogeneity but others use the difference in average values. Generally, pairs of regions are compared, allowing more complex shapes to emerge.
A program in use at Heriot-Watt is spam ( split and merge) which takes regions a pair at a time and uses the
difference of averages to judge similarity, i.e. merge region A with neighbouring region B if the difference in average intensities of A and B is below a threshold.
Algorithm for successive region merging
Put all regions on ProcessList
Repeat
Extract each region from ProcessList
Traverse remainder of list to find similar region (homogeneity criterion)
If they are neighbours then
merge the regions and recalculate property values;
until (no merges are possible)
Figure 2 illustrates this split-and-merge algorithm applied to a picture of a cup and a light bulb.

Figure 2: Regional segmentation by splitting and merging

Figure 3: Regional segmentation by splitting and merging
Problems and comparison with boundary segmentation
There are problems with regional segmentation of any form:
-
``Meaningful'' regions may not be uniform: surface properties of a solid body will vary in brightness or colour dependent on the existence of slowly varying gradients due to lighting conditions. Lighting effects or curvature affect the appearance, e.g. a sphere illuminated by a point light source may have intensities varying from pure white to black, yet is a single surface.
-
It is very unusual in practice for an image to be composed of uniform regions of similar intensity, or colour, or texture etc.
-
Regional segmentation works best with binary data as the limited range of values lead to more uniform regions.
In practice, boundary segmentation is much more widely applied than regional segmentation for several reasons.
-
Algorithms are usually less complex: they tend to use local properties and software and hardware implementations are readily available.
-
Humans may use edge detection: there is evidence of links between edge detection and early human visual processing, which lead to the observation that contoured images are more easily identified than regional images, particularly when degraded in some form.
-
Edges are often more useful in matching: as finding regions or edges is often preliminary to identifying objects, it is important that edges have an easier model description (as lines).
Nevertheless there are several situations where a regional description is more appropriate, particularly when texture or ``edginess''
is in itself a regional property.



[ Region growing: a recursive approach |
Regional Representation ]
Comments to: Sarah Price at ICBL.
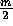 by
by 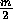 below it in the pyramid. Usually the algorithm starts from the initial assumption that the entire image is a single region, then computes the homogeneity criterion to see if it is TRUE. If FALSE, then the square region is split into the four smaller regions. This process is then repeated on each of the sub-regions until no further splitting is necessary. These small square regions are then merged if they are similar to give larger irregular regions. The problem (at least from a programming point of view) is that any two regions may be merged if adjacent and if the larger region satisfies the homogeneity criteria, but regions which are adjacent in image space may have different parents or be at different levels (i.e. different in size) in the pyramidal structure. The process terminates when no further merges are possible.
below it in the pyramid. Usually the algorithm starts from the initial assumption that the entire image is a single region, then computes the homogeneity criterion to see if it is TRUE. If FALSE, then the square region is split into the four smaller regions. This process is then repeated on each of the sub-regions until no further splitting is necessary. These small square regions are then merged if they are similar to give larger irregular regions. The problem (at least from a programming point of view) is that any two regions may be merged if adjacent and if the larger region satisfies the homogeneity criteria, but regions which are adjacent in image space may have different parents or be at different levels (i.e. different in size) in the pyramidal structure. The process terminates when no further merges are possible. 


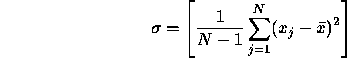
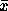 is the mean intensity of the N pixels in the region.
Whereas splitting is quite simple, merging is more complex. Different algorithms are possible, some use the same test for homogeneity but others use the difference in average values. Generally, pairs of regions are compared, allowing more complex shapes to emerge.
is the mean intensity of the N pixels in the region.
Whereas splitting is quite simple, merging is more complex. Different algorithms are possible, some use the same test for homogeneity but others use the difference in average values. Generally, pairs of regions are compared, allowing more complex shapes to emerge.




