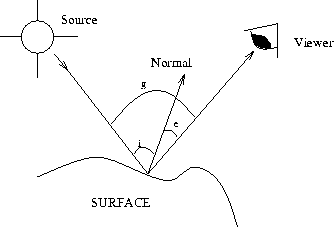
Figure 2: Incident and reflected light on a surface
The amount of light reflected by a surface element depends on the material. For most surfaces the fraction of incident illumination depends only on surface orientation. The reflectance properties of such a surface can be represented as a function f( i, e, g ) of the three angles i,e and g defined in Figure 2, below.
Figure 2: Incident and reflected light on a surface
) incident on the surface.
The amount of light radiated from a surface is called the radiance.
It is the power per unit area per unit solid angle (
)
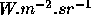emitted from the surface. The reflectance
function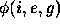 
determines the ratio of surface
radiance to irradiance measured per unit surface area per
unit solid angle, in the direction of the viewer.
Consider the example of a perfect specular or mirror like reflection.
The reflectance function 
can be obtained as follows :
All the reflected light can be viewed for a single direction only, where the incident and emergent angles are equal. Perfect mirror surfaces are rare; in general the intersection of light with surfaces of varying roughness and material composition leads to a more complex spatial distribution of reflected light, for example as a combination of a forescatter lobe (distributed about the direction of specular reflection), a normal lobe (distributed about the normal ) and a backscatter lobe (distributed about the incident direction). Commonly, a simple approximation is that of a perfectly diffuse ( Lambertian) surface which appears equally bright from all viewing directions,
where 
is the albedo or reflectance factor and 
is the incident
light intensity. The cosine of the incident angle represents the foreshortening
of the surface from the direction of the source. As the source rotates closer to
the normal direction, so more light falls on the surface per unit area; hence it
appears brighter.
The brightness does not depend on the viewing direction (through e or g).
[ Surface orientation and gradient space |
The Reflectance Map and the Image Irradiance Equation
]
Comments to: Sarah Price at ICBL.
