Relaxation Labelling

Relaxation labelling techniques can be applied to many areas of computer vision.

Relaxation techniques have been applied to many other areas of computation in general, particularly to the solution of simultaneous nonlinear equations.

We shall first describe the basic principles behind relaxation labelling methods and then discuss various applications.

The basic elements of the relaxation labelling method are a set of features belonging to an object and a set of labels.

In the context of vision, these features are usually points, edges and surfaces.

Normally, the labelling schemes used are probabilistic in that for each feature, weights or probabilities are assigned to each label in the set giving an estimate of the likelihood that the particular label is the correct one for that feature.

Probabilistic approaches are then used to maximise (or minimise) the probabilities by iterative adjustment, taking into account the probabilities associated with neighbouring features.

Relaxation strategies do not necessarily guarantee convergence, and thus, we may not arrive at a final labelling solution with a unique label having probability one for each feature.

Let us now consider the labelling approach in more detail. Let us assume:

• O is the set of n object features to be labelled.
• L is the set of m possible labels for the features.

Let be the probability that the label is the correct label for object feature .

The usual probability axioms can be applied that:

• Each probability satisfies where implies that label is impossible for feature and implies that this labelling is certain.
• The set of labels are mutually exclusive and exhaustive. Thus we may write for each i:
  
  Thus each feature is correctly described by exactly one label from the set of labels.

The labelling process starts with an initial, and perhaps arbitrary, assignment of probabilities for each label for each feature.

The basic algorithm then transforms these probabilities into to a new set according to some relaxation schedule.

This process is repeated until the labelling method converges or stabilises.

This occurs when little or no change occurs between successive sets of probability values.

Popular methods often take stochastic approaches to update the probability functions.

Here an operator considers the compatibility of label probabilities as constraints in the labelling algorithm.

The compatibility is a correlation between labels defined as the conditional probability that feature has a label given that feature has a label , i.e. .

Thus, updating the probabilities of labels is done by considering the probabilities of labels for neighbouring features.

Let us assume that we have changed all probabilities up to some step, S, and we now seek an updated probability for the next step S+1.

We can estimate the change in confidence of by:
 
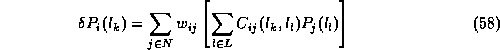
where N is the set of features neighbouring , and is a factor that weights the labellings of these neighbours, defined in such a way that

The new probability for label in generation S+1 can be computed from the values from generation S using

 
• Statistical Relaxation Techniques