


Next: Derivation of Kruppa's Equations
Up: Self Calibration
Previous: Self Calibration
Consider two camera projections P and P' corresponding to the same
camera (internal parameters) but different poses. We saw in exercise
4.3 that the image of the absolute conic (IAC) is independent of
the camera pose. In fact, the IAC is directly related to the internal
parameter matrix K of the camera defined in equation
(1.2).
Given that the absolute conic is in any case invariant under
rotations and translations, we can choose coordinates so that the
first projection matrix reduces to
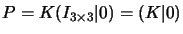 (c.f. equation
1.1). Hence, for a point
(c.f. equation
1.1). Hence, for a point
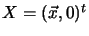 on the plane at infinity we have projection
on the plane at infinity we have projection
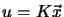 or
or
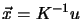 .
.
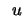 is on the image of the absolute
conic exactly when X is on the conic itself, i.e. when
is on the image of the absolute
conic exactly when X is on the conic itself, i.e. when
So the image of the absolute conic is given by the matrix
K-tK-1. If this matrix can be found, by Choleski factorization
we can extract K-1 and thence find the internal parameter matrix
K. In fact, as we will see, it is easier to work from the outset
with the inverse KtK of the IAC matrix, called the dual image
of the absolute conic (DIAC).



Next: Derivation of Kruppa's Equations
Up: Self Calibration
Previous: Self Calibration
Bill Triggs
1998-11-13
![]() (c.f. equation
1.1). Hence, for a point
(c.f. equation
1.1). Hence, for a point
![]() on the plane at infinity we have projection
on the plane at infinity we have projection
![]() or
or
![]() .
.
![]() is on the image of the absolute
conic exactly when X is on the conic itself, i.e. when
is on the image of the absolute
conic exactly when X is on the conic itself, i.e. when