
Up: Computer Vision IT412
Previous: Image rectification
Given a point m that has coordinates (u1,v1)
in the first retinal plane  ,it is known that its correspondence and the
fundamental matrix are related by:
,it is known that its correspondence and the
fundamental matrix are related by:
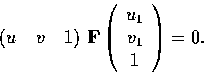
This equation can be expanded to
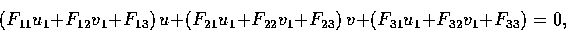
where u1 and v1 are known entities, u and v are variables.
This is the equation of a line in the second retinal plane.
It is the epipolar line on which m' must lie.
Given a point m that has coordinates (u1,v1)
in the first retinal plane 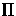 ,to compute the epipolar line l
,to compute the epipolar line l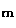 that contains m,
we must first compute the epipole e
that contains m,
we must first compute the epipole e 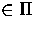 .
.
e 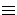 intersection point of all epipolar lines in
intersection point of all epipolar lines in  .
.
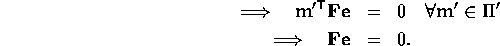
- The epipole e in
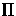
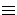 projection
of C' onto
projection
of C' onto 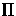
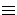 null vector of F.
null vector of F.
- The epipole
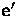 in
in 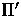
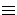 projection
of C onto
projection
of C onto 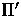
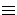 null vector of F
null vector of F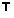 .
.
The coordinates of l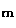 can then be computed as
the cross-product of e and m.
can then be computed as
the cross-product of e and m.
Robyn Owens
10/29/1997
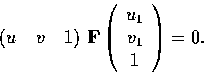
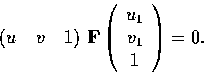
![]()
![]() ,to compute the epipolar line l
,to compute the epipolar line l![]() that contains m,
we must first compute the epipole e
that contains m,
we must first compute the epipole e ![]() .
.![]() intersection point of all epipolar lines in
intersection point of all epipolar lines in ![]() .
.
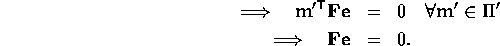
![]() can then be computed as
the cross-product of e and m.
can then be computed as
the cross-product of e and m.