Image decomposition

Once the phase congruency map of an image has been constructed we know the feature structure of the image. As was mentioned above, the standard way of compressing this feature structure is to apply a threshold, thus reducing a rich image representation to a simple binary structure. However, thresholding is course, highly subjective, and in the end eliminates much of the important information in the image.

Some other method of compressing the feature information needs to be considered, and some way of extracting the non-feature information, or the smooth map of the image, needs to be developed. In the absence of noise, the feature map and the smooth map should comprise the whole image. When noise is present, there will be a third component to any image signal, and one that is independent of the other two. This approach was developed by Aw [1,2] in his thesis and used to develop an image compression technique that works very effectively on images with fine feature detail, where the standard algorithms like JPEG fail to maintain image fidelity.

To decompose an image into its component structures, we must first understand the non-linear nature of the local energy feature model. When two image signals, both with features, are considered, a combined image signal should contain the image structure of both these signals. And if two image signals, both without features, are combined then the resulting perception should be an image without features. These constraints impose a certain type of feature stability on the process of image perception.

However, if we simply add images together, some feature structure might cancel out or be created, so that the underlying features would be lost. To see this, consider adding two sine waves together, where the sine waves have different frequencies, say $\sin(x)$ and $\sin(3x)$. Now both sine waves individually have no feature structure, since the Hilbert transform of $\sin$ is $\cos$ and $\sin^2(x) + \cos^2(x) = 1$. However, the waveform $\sin(x) + \sin(3x)$does have features, precisely at the point where beating occurs between the two waves. Under the local energy model, this is exactly what is predicted, since the energy of the added waveforms is

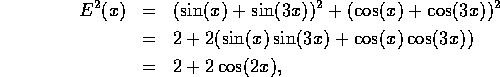
and this energy function has peaks at the peaks of the cosine term.

Now is this non-linearity a problem? We know, from psychophysical experiments, that humans demonstrate a perception known as frequency doubling. When shown two sine waves, one completely out of phase with the other and the images alternating rapidly before the viewer, humans don't perceive a uniform flat image, as would be the case if they simply added the two image signals. Rather, they see another wave of twice the frequency. Such a phenomenon can not be explained by assuming an underlying linear system for visual perception. However, the local energy model predicts exactly this perception.

To see how this is so, we have to define how images are combined within the local energy model. Instead of simple addition, local energy postulates an image combination operator that simulates complex multiplication. Two image signals, f and g, are initially imagined as the real parts of two complex images signals, $f + i \tilde{f}$ and $g + i \tilde{g}$. These two complex signals can be multiplied together in the usual way, and the resulting signal would have real part $fg - \tilde{f} \tilde{g}$ whilst the imaginary part would be $\tilde{f} g + f \tilde{g}$. We define our new image combination as the real part of the complex images combined using complex multiplication:

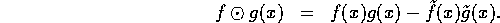
In a similar fashion, and again by analogy with complex division, the inverse operator is defined by

$$f \oslash g(x) = \frac{f(x)g(x) + \tilde{f}(x) \tilde{g}(x)}{g^2(x) + \tilde{g}^2(x)}.$$

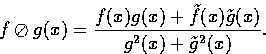
With these definitions, we can now prove the following theorem:

THEOREM: The phase congruency map of an image uniquely defines the image luminance function, apart from a feature-free profile.

Proof: We first show how energy distributes over the $\odot$ operator.

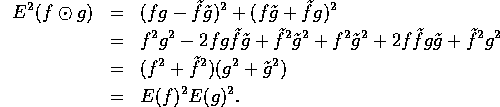
Now if two image signals f and g have the same phase congruency map, then we know that their energy functions are scalar multiples of each other, that is E(f) = cE(g), for some constant c. In this case

and so $f \oslash g$ is a feature-free image because its energy function has no local maxima.

Returning to the phenomenon of frequency doubling, we now see that the image combination of the two sine waves is in fact a cosine wave of twice the frequency. For

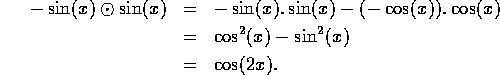
We can also deduce from this theorem that given any image signal f, once we have calculated its phase congruency map PC we can also calculate its smooth map S by simply calculating

$$S(x) = f(x) \oslash PC(x).$$

The component S(x) contains all the non-feature information of the image, and PC contains all the feature information. Together, they re-combine to form the original image, that is, $f(x) = PC(x) \odot S(x)$.

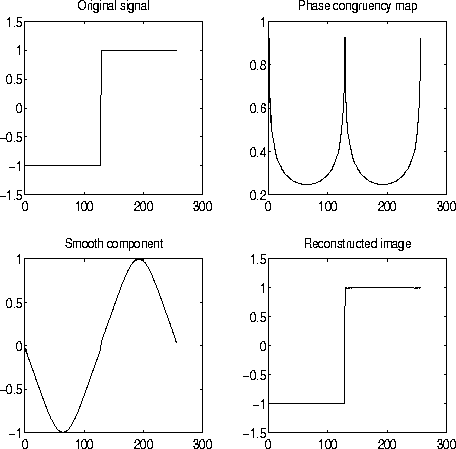
Figure 11 illustrates this process for a synthetic step wave, and figure 12 shows the same information for a real image signal (and thus one that contains some noise). We see that we have a way of decomposing any image signal into its featured and smooth components, and that these components contain all the information in the signal in the sense that the original signal can be reconstructed from them.

 

Figure 11: a) The step profile. b) Its phase congruency map. c) Its smooth map. d) The reconstruction of the step signal.

 

Figure 12: a) A real image. b) Its phase congruency map. c) Its smooth map. d) The reconstruction of the image.