The Earth Mover's Distance (EMD) is a method to evaluate dissimilarity between two multi-dimensional distributions in some feature space where a distance measure between single features, which we call the ground distance is given. The EMD ``lifts'' this distance from individual features to full distributions.
Intuitively, given two distributions, one can be seen as a mass of earth properly spread in space, the other as a collection of holes in that same space. Then, the EMD measures the least amount of work needed to fill the holes with earth. Here, a unit of work corresponds to transporting a unit of earth by a unit of ground distance.
A distribution can be represented by a set of clusters where each cluster is represented by its mean (or mode), and by the fraction of the distribution that belongs to that cluster. We call such a representation the signature of the distribution. The two signatures can have different sizes, for example, simple distributions have shorter signatures than complex ones.
Computing the EMD is based on a solution to the well-known transportation problem [1]. Suppose that several suppliers, each with a given amount of goods, are required to supply several consumers, each with a given limited capacity. For each supplier-consumer pair, the cost of transporting a single unit of goods is given. The transportation problem is then to find a least-expensive flow of goods from the suppliers to the consumers that satisfies the consumers' demand. Matching signatures can be naturally cast as a transportation problem by defining one signature as the supplier and the other as the consumer, and by setting the cost for a supplier-consumer pair to equal the ground distance between an element in the first signature and an element in the second. Intuitively, the solution is then the minimum amount of ``work'' required to transform one signature into the other.
This can be formalized as the following linear programming problem:
Let
![]() be the first signature
with m clusters, where pi is the cluster representative and
wpi is the weight of the cluster;
be the first signature
with m clusters, where pi is the cluster representative and
wpi is the weight of the cluster;
![]() the second signature with
n clusters; and
the second signature with
n clusters; and
![]() the ground distance matrix where
dij is the ground distance between clusters pi and qj.
the ground distance matrix where
dij is the ground distance between clusters pi and qj.
We want to find a flow
![]() ,
with fij the flow
between pi and qj, that minimizes the overall cost
,
with fij the flow
between pi and qj, that minimizes the overall cost
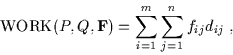
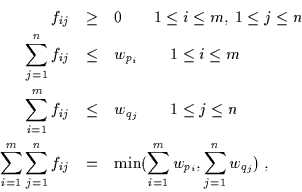
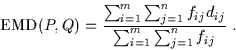
The EMD has the following advantages
More details on the EMD can be found in [2].