Gabor Filters
Gabor filters are bandpass filters which are used in image processing for
feature extraction, texture analysis [1]
, and stereo disparity estimation [9,10,13-15,24,30].
The impulse response of these filters is created by multiplying an Gaussian
envelope function with a complex oscillation. Gabor [11]
showed that these elementary functions minimize the space (time)-uncertainty
product. By extending these functions to two dimensions it is possible
to create filters which are selective for orientation [7]
. Under certain conditions the phase of the response of Gabor filters is
approximately linear. This property is exploited by stereo approaches which
use the phase-difference of the left and right filter responses to estimate
the disparity in the stereo images [9,10,13-15,24,30].
It was shown by several researchers that the profile of simple-cell
receptive fields in the mammalian cortex can by discribed by oriented two-dimensional
Gabor functions [2,3,6,8,16-20,22,23,25-29].
Let x=[x1 x2]T
be the image coordinates. The impulse response of a Gabor filter g(x)
is then given by:
Here, the matix A determines the bandwidth and the orientation
selectivity of the filter.
If the modulation frequency vektor k0 is in the
same direction as one of the envelopes axes, with
then the real part and the imaginary part of the filter's impulse response
are looking as follows:
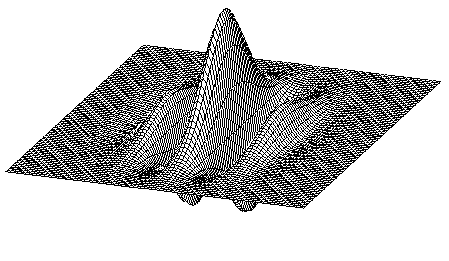
Real part and imaginary part of the impulse response
of a Gabor filter
The transfer function G(k) of a Gabor filter (Fourier
transform of the impulse response) is given by:
where k = [k1 k2]T
is the spatial frequency. In oder to establish a multi-resolution strategy
the image can be filtered with a set of N Gabor filters with
different bandwidths and modulation frequencies. If the modulation frequencies
are given by
and the relative bandwidth is choosen to be constant for all filters the
image is decomposed into octaves.
Magnitude of a Gabor filter set for N=4 in
direction of the modulation frequency
In the figure shown above the transfer functions of the filters are
choosen to overlap at a value of 0.5. Under this condition the DC component
in the images and the frequency components lying above the frequency twice
as large as the modulation freqency are damped by at least -54dB. Thus
the filter results can be sub-sampled by a factor
with neglectable aliasing effects. Furthermore the images can be
decomposed into M channels of different orientations by using filters
tuned to different angles:
Half-value plot of the Gabor filters in the
frequency plane tuned to different frequencies and orientations (30
degree resolution)
The responses of the filters lying in the lower frequency half-plane
need not to be calculated explicitely, because they can be generated by
the complex-conjugation of the filter response lying
on the other side of the origin. The following images show the original
Lenna picture and Gabor filter results for different sampling factors.
The size of the input image is choosen such that the filter results have
always the same size after subsampling. This strategy leads to a multy
resolution architecture which is also called Gabor pyramid. In the
best resolution channel it is possible to extract fine image structures
of a small image region whereas in the lower resolution levels coarse image
structures can be extracted over large regions. This can be exploited in
coarse-to-fine strategies [4,5].
On the left side of the following pictures the original input (sub) images
and the superposed filter results for all orientations are shown. On the
right side the subsampled filter result is shown for each orientation.
s = 4
s = 2
s = 1
Subimages of the Lenna-picture and magnitudes of
the corresponding filter results
We use a set of Gabor filters as a preprocessing step for estimation
of stereo disparity and extraction of oriented image features in the
DEMON
project
Last change: 17.11.1998 (R.Trapp)
