


Next:ExamplesUp:Kernel
Principal Component AnalysisPrevious:Introduction
Implementation
Suppose we have a training set  .
We then have the corresponding set of mapped data points in the feature
space
.
We then have the corresponding set of mapped data points in the feature
space 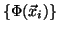 .
We denote centred data points thus:
.
We denote centred data points thus:
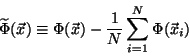
The Kernel PCA algorithm then proceeds as follows:
-
Pick an appropriate kernel function
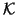 (the form of the kernel, plus any parameters).
(the form of the kernel, plus any parameters).
-
Construct the Kernel Matrix for the mapped data:
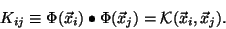
-
Use this to construct the Covariance Matrix for the centred data:

-
Solve for the set of eigenvectors
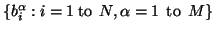 of the matrix
of the matrix 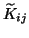 ,
which give us our set of basis vectors
,
which give us our set of basis vectors 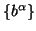 in feature space thus:
in feature space thus:
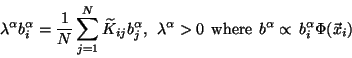
-
The unnormalised KPCA components of a test point
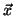 are then given by:
are then given by:
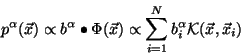
The exact values of the components depend on the normalisation chosen
for the set of vectors 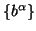 ,
which will always form an orthogonal basis, but need not be orthonormal.
The value of a component can also be shifted so that the mean of each component
over the data is then zero.
,
which will always form an orthogonal basis, but need not be orthonormal.
The value of a component can also be shifted so that the mean of each component
over the data is then zero.



Next:ExamplesUp:Kernel
Principal Component AnalysisPrevious:Introduction
Carole Twining
2001-10-02
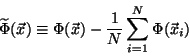
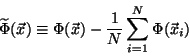

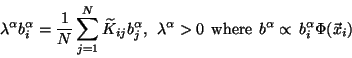
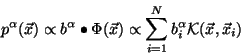
![]() ,
which will always form an orthogonal basis, but need not be orthonormal.
The value of a component can also be shifted so that the mean of each component
over the data is then zero.
,
which will always form an orthogonal basis, but need not be orthonormal.
The value of a component can also be shifted so that the mean of each component
over the data is then zero.