



Next: Free-form Deformation Models
Up: Deformable Template Models
Previous: Bayes' Theorem
In many deformable matching problems, the objective
function consists of two parts:
-
The internal energy, prior, or geometrical information is related only to the
geometric shape of the deformed template (contour) which
is an intrinsic property of the template, independent of
the input image and sensor data.
- In free-form deformation models, this term
corresponds to the regularization constraints on the template, for example,
the elasticity or stretchness.
It is equivalent to a prior which reflects a preference for smooth and
compact contours.
- In the analytic form based deformation models,
where the template is parameterized,
this term is specified in terms of the model parameters, which reflects
either the choice of the parameter values, or the
interactions between different parts of the template.
- In the prototype-based
deformation models, this term is also a function of the deformation
parameters. It biases the choice of the geometric shape. For example,
it can specify the penalty for deviations from the expected shape.
-
The likelihood term, in all the cases, pertains to the input image data.
Via this term, the deformable model interacts with the image, being
attracted to the desired salient image features. This term
measures the
fidelity, or goodness of fit, of the template to the input image.
The deformed template matching which optimizes an objective function leads to an
interpretation of the image.
When the deformable template modeling is cast in the Bayesian framework using
Eq. (1), the prior model  typically imposes the geometrical
preferences of the shape model. It is related to the internal energy term, which is a measure of the geometrical
structure on a deformed template or contour.
The imaging model
typically imposes the geometrical
preferences of the shape model. It is related to the internal energy term, which is a measure of the geometrical
structure on a deformed template or contour.
The imaging model 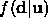 is a description of the noisy or
stochastic process that relates the deformed template to the input image or
sensor values
is a description of the noisy or
stochastic process that relates the deformed template to the input image or
sensor values 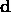 . This likelihood captures the
desired image cues. It is related to the external energy term, which describes the
interaction between the template and the image.
Bayes' rule combines these two probabilistic models to
form a posterior probability
. This likelihood captures the
desired image cues. It is related to the external energy term, which describes the
interaction between the template and the image.
Bayes' rule combines these two probabilistic models to
form a posterior probability 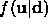 which describes
the best estimate of
which describes
the best estimate of 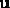 given the data
given the data  and prior knowledge
and prior knowledge 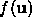 . Note that
. Note that  is
a constant, given
is
a constant, given 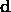 . Therefore, maximizing the posteriori density in
Eq. (1) is equivalent to maximizing the product
. Therefore, maximizing the posteriori density in
Eq. (1) is equivalent to maximizing the product  .
.




Next: Free-form Deformation Models
Up: Deformable Template Models
Previous: Bayes' Theorem
Bob Fisher
Wed May 5 18:16:24 BST 1999
 typically imposes the geometrical
preferences of the shape model. It is related to the internal energy term, which is a measure of the geometrical
structure on a deformed template or contour.
The imaging model
typically imposes the geometrical
preferences of the shape model. It is related to the internal energy term, which is a measure of the geometrical
structure on a deformed template or contour.
The imaging model 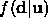 is a description of the noisy or
stochastic process that relates the deformed template to the input image or
sensor values
is a description of the noisy or
stochastic process that relates the deformed template to the input image or
sensor values 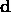 . This likelihood captures the
desired image cues. It is related to the external energy term, which describes the
interaction between the template and the image.
Bayes' rule combines these two probabilistic models to
form a posterior probability
. This likelihood captures the
desired image cues. It is related to the external energy term, which describes the
interaction between the template and the image.
Bayes' rule combines these two probabilistic models to
form a posterior probability 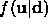 which describes
the best estimate of
which describes
the best estimate of 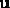 given the data
given the data  and prior knowledge
and prior knowledge 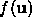 . Note that
. Note that  is
a constant, given
is
a constant, given 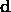 . Therefore, maximizing the posteriori density in
Eq. (1) is equivalent to maximizing the product
. Therefore, maximizing the posteriori density in
Eq. (1) is equivalent to maximizing the product  .
.



