Common Names: Median filtering, Rank filtering
The median filter is normally used to reduce noise
in an image, somewhat like the mean filter. However, it often does a
better job than the mean filter of preserving useful detail in the
image.
Like the mean filter, the median filter considers each pixel in the image in turn and looks at its nearby neighbors to decide whether or not it is representative of its surroundings. Instead of simply replacing the pixel value with the mean of neighboring pixel values, it replaces it with the median of those values. The median is calculated by first sorting all the pixel values from the surrounding neighborhood into numerical order and then replacing the pixel being considered with the middle pixel value. (If the neighborhood under consideration contains an even number of pixels, the average of the two middle pixel values is used.) Figure 1 illustrates an example calculation.
Figure 1 Calculating the median value of a pixel neighborhood. As can be seen, the central pixel value of 150 is rather unrepresentative of the surrounding pixels and is replaced with the median value: 124. A 3×3 square neighborhood is used here --- larger neighborhoods will produce more severe smoothing.
By calculating the median value of a neighborhood rather than the mean filter, the median filter has two main advantages over the mean filter:
The image
shows an image that has been corrupted
by Gaussian noise with mean 0 and standard deviation
(
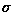) 8. The original image is
for comparison. Applying a 3×3 median filter produces
Note how the noise has been reduced at the expense of a slight degradation in image quality. The image
has been corrupted by even more noise (Gaussian
noise with mean 0 and 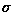13), and
is the result of 3×3 median filtering. The median filter is sometimes not as subjectively good at dealing with large amounts of Gaussian noise as the mean filter.
Where median filtering really comes into its own is when the noise produces extreme `outlier' pixel values, as for instance in
which has been corrupted with `salt and pepper' noise, i.e. bits have been flipped with probability 1%. Median filtering this with a 3×3 neighborhood produces
in which the noise has been entirely eliminated with almost no degradation to the underlying image. Compare this with the similar test on the mean filter.
Consider another example wherein the original image
has been corrupted with higher levels (i.e. p=5% that a bit is flipped) of salt and pepper noise
After smoothing with a 3×3 filter, most of the noise has been eliminated
If we smooth the noisy image with a larger median filter, e.g. 7×7, all the noisy pixels disappear, as shown in
Note that the image is beginning to look a bit `blotchy', as graylevel regions are mapped together. Alternatively, we can pass a 3×3 median filter over the image three times in order to remove all the noise with less loss of detail
In general, the median filter allows a great deal of high spatial frequency detail to pass while remaining very effective at removing noise on images where less than half of the pixels in a smoothing neighborhood have been effected. (As a consequence of this, median filtering can be less effective at removing noise from images corrupted with Gaussian noise.)
One of the major problems with the median filter is that it is relatively expensive and complex to compute. To find the median it is necessary to sort all the values in the neighborhood into numerical order and this is relatively slow, even with fast sorting algorithms such as quicksort. The basic algorithm can, however,be enhanced somewhat for speed. A common technique is to notice that when the neighborhood window is slid across the image, many of the pixels in the window are the same from one step to the next, and the relative ordering of these with each other will obviously not have changed. Clever algorithms make use of this to improve performance.
You can interactively experiment with this operator by clicking here.
explore the effect of median filtering with different neighborhood sizes.
Illustrate this to yourself by performing smoothing and pixel addition (in the order indicated on each side of the above equation!) to a set of test images. Carry out this experiment on some simple images, e.g.
and
R. Boyle and R. Thomas Computer Vision: A First Course, Blackwell Scientific Publications, 1988, pp 32 - 34.
E. Davies Machine Vision: Theory, Algorithms and Practicalities, Academic Press, 1990, Chap. 3.
A. Marion An Introduction to Image Processing, Chapman and Hall, 1991, p 274.
D. Vernon Machine Vision, Prentice-Hall, 1991, Chap. 4.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
