Color Quantization

Color quantization is applied when the color information of an image is to be reduced. The most common case is when a 24-bit color image is transformed into an 8-bit color image.

Two decisions have to be made:

which colors of the larger color set remain in the new image, and
how are the discarded colors mapped to the remaining ones.

The simplest way to transform a 24-bit color image into 8 bits is to assign 3 bits to red and green and 2 bits to blue (blue has only 2 bits, because of the eye's lower sensitivity to this color). This enables us to display 8 different shades of red and green and 4 of blue. However, this method can yield only poor results. For example, an image might contain different shades of blue which are all clustered around a certain value such that only one shade of blue is used in the 8-bit image and the remaining three blues are not used.

Alternatively, since 8-bit color images are displayed using a colormap, we can assign any arbitrary color to each of the 256 8-bit values and we can define a separate colormap for each image. This enables us perform a color quantization adjusted to the data contained in the image. One common approach is the popularity algorithm, which creates a histogram of all colors and retains the 256 most frequent ones. Another approach, known as the median-cut algorithm, yields even better results but also needs more computation time. This technique recursively fits a box around all colors used in the RGB colorspace which it splits at the median value of its longest side. The algorithm stops after 255 recursions. All colors in one box are mapped to the centroid of this box.

All above techniques restrict the number of displayed colors to 256. A technique of achieving additional colors is to apply a variation of half-toning used for gray scale images, thus increasing the color resolution at the cost of spatial resolution. The 256 values of the colormap are divided into four sections containing 64 different values of red, green, blue and white. As can be seen in Figure 1, a 2×2 pixel area is grouped together to represent one composite color, each of the four pixels displays either one of the primary colors or white. In this way, the number of possible colors is increased from 256 to 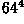Eqn:eqnquant .

Figure 1 A 2×2 pixel area displaying one composite color.