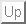

Consider a parametric vector equation of a curve:

where u is an arbitrary parameter. In many shape descriptors, the curve is reparametrised by normalised arc length, s which is defined as follows.
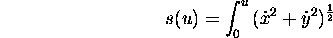
Arc length is preserved under similarity transforms ie the corresponding points between the original and the transformed curve have the same normalised arc length under change in orientation, translation, and differ by a scale factor under scaling.
Arc length is not preserved under general affine transforms:
where 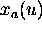 and
and 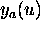 represent the coordinates of the transformed
curve.
represent the coordinates of the transformed
curve.
In some applications, where curves are subject to general affine transforms, arc length is replaced by affine length which is defined as follows and is proved to be affine-invariant.
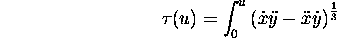
The corresponding points differ by a scale factor which is  , and A is called the transformation matrix,
, and A is called the transformation matrix,
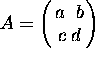 .
.
Curvature has been proved to be a very useful shape descriptor which can be computed as:
If arc length, s, is used to parameterize the curve, the formula for curvature will be as follows.
Curvature is invariant under similarity transforms. It remains unchanged under rotation and translation; and its value under uniform scaling is inversely proportional to the scale factor. However, under general affine transforms, the change in curvature is not a linear function of the transformation matrix. Affine curvature has been defined as an alternative for curvature which changes linearly under affine transforms.
The definition of affine curvature is based on affine length 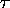 ,
as follows:
,
as follows:
Note the similarity of equations (4) and (3). It is much easier to compute affine curvature if it is expressed as a function of an arbitrary parameter.
where 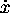 ,
, 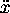 ,
, 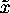 and
and 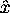 denote the first, second, third, and fourth
derivatives of x with respect to u, respectively. Derivatives of y are defined similarly.
denote the first, second, third, and fourth
derivatives of x with respect to u, respectively. Derivatives of y are defined similarly.
The following facts can be observed from this equation.
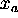 and
and 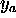 from equation (1), we obtain the following
result:
from equation (1), we obtain the following
result:
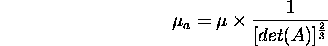
where  and
and 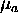 denote affine curvature on the original and affine
transformed curve respectively and det denotes determinant. The difference
between the affine curvature of the original and affine transformed shape
is represented by a scale factor.
denote affine curvature on the original and affine
transformed curve respectively and det denotes determinant. The difference
between the affine curvature of the original and affine transformed shape
is represented by a scale factor.