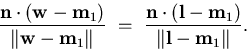Next: Numerical Results for the
Up: Defocus Blur of a
Previous: Defocus Blur of a
To analyze defocus blur, we need to work in 3-D. We
use the 3-D cartesian frame 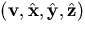 where
where 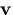 is the location of the effective
viewpoint,
is the location of the effective
viewpoint, 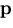 is the location of the effective pinhole,
is the location of the effective pinhole,
 is a unit vector in the direction
is a unit vector in the direction
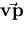 , the effective pinhole is located
at a distance c from the effective viewpoint, and the vectors
, the effective pinhole is located
at a distance c from the effective viewpoint, and the vectors
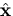 and
and 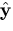 are orthogonal unit vectors
in the plane z=0. As in Section 3, we also assume that
the conventional camera used in the catadioptric sensor has a frontal
image plane located at a distance u from the pinhole and that the
optical axis of the camera is aligned with the z-axis. In addition
to the previous assumptions, we assume that the effective pinhole of
the lens is located at the center of the lens, and that the lens has
a circular aperture. See Figure 9 for an illustration
of this configuration.
are orthogonal unit vectors
in the plane z=0. As in Section 3, we also assume that
the conventional camera used in the catadioptric sensor has a frontal
image plane located at a distance u from the pinhole and that the
optical axis of the camera is aligned with the z-axis. In addition
to the previous assumptions, we assume that the effective pinhole of
the lens is located at the center of the lens, and that the lens has
a circular aperture. See Figure 9 for an illustration
of this configuration.
Consider a point 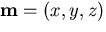 on the mirror and a point
on the mirror and a point
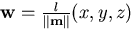 in the world, where
in the world, where
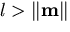 . Then, since the hyperboloid mirror satisfies
the fixed viewpoint constraint, a ray of light from
. Then, since the hyperboloid mirror satisfies
the fixed viewpoint constraint, a ray of light from 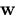 which is
reflected by the mirror at
which is
reflected by the mirror at 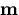 passes directly through the
center of the lens (i.e. the effective pinhole.) This ray of light is
known as the principal ray [Hecht and Zajac, 1974]. Next, suppose
a ray of light from the world point
passes directly through the
center of the lens (i.e. the effective pinhole.) This ray of light is
known as the principal ray [Hecht and Zajac, 1974]. Next, suppose
a ray of light from the world point 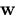 is reflected at the point
is reflected at the point 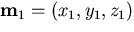 on
the mirror and then passes through the lens point
on
the mirror and then passes through the lens point 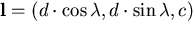 . In general, this
ray of light will not be imaged at the same point on the image plane
as the principal ray. When this happens there is defocus blur.
The locus of the intersection of the incoming rays through
. In general, this
ray of light will not be imaged at the same point on the image plane
as the principal ray. When this happens there is defocus blur.
The locus of the intersection of the incoming rays through
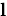 and the image plane as
and the image plane as 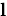 varies over the lens is
known as the blur region or region of confusion
[Hecht and Zajac, 1974]. For an ideal thin lens in isolation, the blur
region is circular and so is often referred to as the blur circle
[Hecht and Zajac, 1974].
varies over the lens is
known as the blur region or region of confusion
[Hecht and Zajac, 1974]. For an ideal thin lens in isolation, the blur
region is circular and so is often referred to as the blur circle
[Hecht and Zajac, 1974].
If we know the points 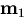 and
and 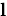 , we can find
the point on the image plane where the ray of light through these
points is imaged. First, the line through
, we can find
the point on the image plane where the ray of light through these
points is imaged. First, the line through 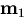 in the
direction
in the
direction  is extended to intersect
the focused plane. By the thin lens law [Hecht and Zajac, 1974]
the focused plane is:
is extended to intersect
the focused plane. By the thin lens law [Hecht and Zajac, 1974]
the focused plane is:
|  |
(40) |
where f is the focal length of the lens and u is the
distance from the focal plane to the image plane.
Since all points on the focused plane are perfectly focused, the
point of intersection on the focused plane can be mapped
onto the image plane using perspective projection. Hence, the x and
y coordinates of the intersection of the ray through 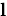 and the image plane are the x and y coordinates of:
and the image plane are the x and y coordinates of:
|  |
(41) |
and the z coordinate is the z coordinate of the image plane c+u.
Given the lens point
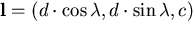 and the world point
and the world point
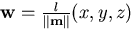 ,there are three constraints on the point
,there are three constraints on the point 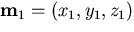 . First,
. First, 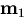 must lie on the
mirror and so (for the hyperboloid) we have:
must lie on the
mirror and so (for the hyperboloid) we have:
|  |
(42) |
Secondly, the incident ray (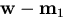 ), the
reflected ray (
), the
reflected ray (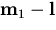 ), and the normal to
the mirror at
), and the normal to
the mirror at 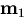 must lie in the same plane.
The normal to the mirror at
must lie in the same plane.
The normal to the mirror at 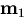 lies in the
direction:
lies in the
direction:
| ![\begin{displaymath}
\mathbf{n} \ = \
\left( [k-2] x_{1}, [k-2] y_{1}, c - 2 z_{1} \right)\end{displaymath}](img133.gif) |
(43) |
for the hyperboloid.
Hence, the second constraint is:
|  |
(44) |
Finally, the angle of incidence must equal the angle of reflection
and so the third constraint on the point 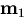 is:
is:
| 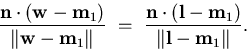 |
(45) |
These three constraints on 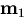 are all multivariate
polynomials in x1, y1, and z1: Equation (44)
and Equation (46) are both of order 2, and
Equation (47) is of order 5. We were unable to find a closed
form solution to these three equations (Equation (47) has 25
terms in general and so it is probable that none exists) but we did
investigate numerical solutions, the results of which are presented
in the following section.
are all multivariate
polynomials in x1, y1, and z1: Equation (44)
and Equation (46) are both of order 2, and
Equation (47) is of order 5. We were unable to find a closed
form solution to these three equations (Equation (47) has 25
terms in general and so it is probable that none exists) but we did
investigate numerical solutions, the results of which are presented
in the following section.



Next: Numerical Results for the
Up: Defocus Blur of a
Previous: Defocus Blur of a
Simon Baker
1/22/1998
![]() on the mirror and a point
on the mirror and a point
![]() in the world, where
in the world, where
![]() . Then, since the hyperboloid mirror satisfies
the fixed viewpoint constraint, a ray of light from
. Then, since the hyperboloid mirror satisfies
the fixed viewpoint constraint, a ray of light from ![]() which is
reflected by the mirror at
which is
reflected by the mirror at ![]() passes directly through the
center of the lens (i.e. the effective pinhole.) This ray of light is
known as the principal ray [Hecht and Zajac, 1974]. Next, suppose
a ray of light from the world point
passes directly through the
center of the lens (i.e. the effective pinhole.) This ray of light is
known as the principal ray [Hecht and Zajac, 1974]. Next, suppose
a ray of light from the world point ![]() is reflected at the point
is reflected at the point ![]() on
the mirror and then passes through the lens point
on
the mirror and then passes through the lens point ![]() . In general, this
ray of light will not be imaged at the same point on the image plane
as the principal ray. When this happens there is defocus blur.
The locus of the intersection of the incoming rays through
. In general, this
ray of light will not be imaged at the same point on the image plane
as the principal ray. When this happens there is defocus blur.
The locus of the intersection of the incoming rays through
![]() and the image plane as
and the image plane as ![]() varies over the lens is
known as the blur region or region of confusion
[Hecht and Zajac, 1974]. For an ideal thin lens in isolation, the blur
region is circular and so is often referred to as the blur circle
[Hecht and Zajac, 1974].
varies over the lens is
known as the blur region or region of confusion
[Hecht and Zajac, 1974]. For an ideal thin lens in isolation, the blur
region is circular and so is often referred to as the blur circle
[Hecht and Zajac, 1974].
![]() and
and ![]() , we can find
the point on the image plane where the ray of light through these
points is imaged. First, the line through
, we can find
the point on the image plane where the ray of light through these
points is imaged. First, the line through ![]() in the
direction
in the
direction ![]() is extended to intersect
the focused plane. By the thin lens law [Hecht and Zajac, 1974]
the focused plane is:
is extended to intersect
the focused plane. By the thin lens law [Hecht and Zajac, 1974]
the focused plane is:
![]() and the world point
and the world point
![]() ,there are three constraints on the point
,there are three constraints on the point ![]() . First,
. First, ![]() must lie on the
mirror and so (for the hyperboloid) we have:
must lie on the
mirror and so (for the hyperboloid) we have: