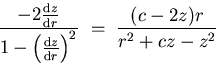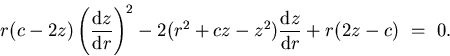Next: General Solution of the
Up: The Fixed Viewpoint Constraint
Previous: The Fixed Viewpoint Constraint
Without loss of generality we can assume that the effective viewpoint
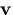 of the catadioptric system lies at the origin of a
cartesian coordinate system. Suppose that the effective pinhole is
located at the point
of the catadioptric system lies at the origin of a
cartesian coordinate system. Suppose that the effective pinhole is
located at the point 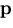 . Then, again without loss of generality,
we can assume that the z-axis
. Then, again without loss of generality,
we can assume that the z-axis  lies in the direction
lies in the direction
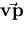 . Moreover, since perspective projection
is rotationally symmetric about any line through
. Moreover, since perspective projection
is rotationally symmetric about any line through 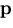 , the
mirror can be assumed to be a surface of revolution about the z-axis
, the
mirror can be assumed to be a surface of revolution about the z-axis
 . Therefore, we work in the 2-D cartesian frame
. Therefore, we work in the 2-D cartesian frame
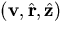 where
where 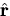 is a unit vector orthogonal to
is a unit vector orthogonal to  , and try to find the
2-dimensional profile of the mirror z(r) = z(x,y) where
, and try to find the
2-dimensional profile of the mirror z(r) = z(x,y) where
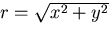 . Finally, if the distance from
. Finally, if the distance from 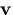 to
to
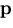 is denoted by the parameter c, we have
is denoted by the parameter c, we have
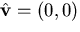 and
and 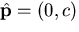 . See
Figure 1 for an illustration
. See
Figure 1 for an illustration![[*]](foot_motif.gif) of the coordinate frame.
of the coordinate frame.
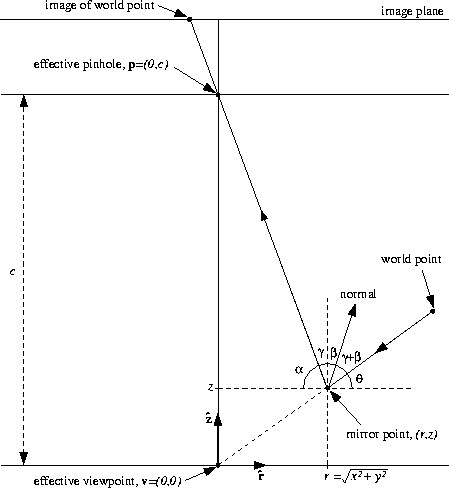
Figure 1:
The geometry used to derive the fixed viewpoint
constraint equation. The viewpoint 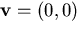 is located
at the
origin of a 2-D coordinate frame
is located
at the
origin of a 2-D coordinate frame 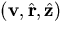 , and the pinhole of the camera
, and the pinhole of the camera 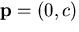 is located at a distance c from
is located at a distance c from
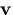 along the z-axis
along the z-axis  .If a ray of light, which was about to pass through
.If a ray of light, which was about to pass through
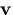 , is reflected at the mirror point (r,z), the angle
between the ray of light and
, is reflected at the mirror point (r,z), the angle
between the ray of light and 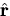 is
is
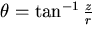 . If the ray is then reflected and passes
through the pinhole
. If the ray is then reflected and passes
through the pinhole 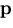 , the angle it makes with
, the angle it makes with
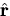 is
is 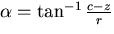 , and the angle
it makes with
, and the angle
it makes with  is
is 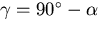 . Finally, if
. Finally, if
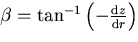 is the angle between the normal to the mirror at (r,z) and
is the angle between the normal to the mirror at (r,z) and
 , then by the fact that the angle of incidence equals
the angle of reflection, we have the constraint that
, then by the fact that the angle of incidence equals
the angle of reflection, we have the constraint that
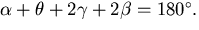
 |
We begin the translation of the fixed viewpoint constraint into
symbols by denoting the angle between an incoming ray from a world
point and the r-axis by 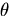 . Suppose that this ray intersects
the mirror at the point (z,r). Then, since we assume that it also
passes through the origin
. Suppose that this ray intersects
the mirror at the point (z,r). Then, since we assume that it also
passes through the origin 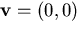 we have the relationship:
we have the relationship:
| 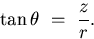 |
(1) |
If we denote the angle between the reflected ray and
the (negative) r-axis by 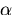 , we also have:
, we also have:
| 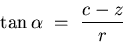 |
(2) |
since the reflected ray must pass through the pinhole 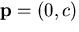 .Next, if
.Next, if  is the angle between the z-axis and the normal to
the mirror at the point (r,z), we have:
is the angle between the z-axis and the normal to
the mirror at the point (r,z), we have:
| 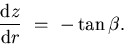 |
(3) |
Our final geometric relationship is due to the fact that we can assume
the mirror to be specular. This means that the angle of incidence
must equal the angle of reflection. So, if 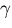 is the
angle between the reflected ray and the z-axis, we have
is the
angle between the reflected ray and the z-axis, we have
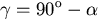 and
and
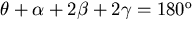 .(See Figure 1 for an illustration of this constraint.)
Eliminating
.(See Figure 1 for an illustration of this constraint.)
Eliminating 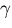 from these two expressions and rearranging
gives:
from these two expressions and rearranging
gives:
| 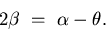 |
(4) |
Then, taking the tangent of both sides and using the standard
rules for expanding the tangent of a sum:
|  |
(5) |
we have:
| 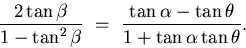 |
(6) |
Substituting from Equations (1), (2), and (3)
yields the fixed viewpoint constraint equation:
| 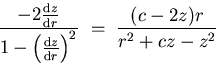 |
(7) |
which when rearranged is seen to be a quadratic first-order ordinary
differential equation:
| 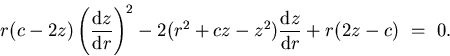 |
(8) |



Next: General Solution of the
Up: The Fixed Viewpoint Constraint
Previous: The Fixed Viewpoint Constraint
Simon Baker
1/22/1998
![[*]](foot_motif.gif) of the coordinate frame.
of the coordinate frame.
![]() of the catadioptric system lies at the origin of a
cartesian coordinate system. Suppose that the effective pinhole is
located at the point
of the catadioptric system lies at the origin of a
cartesian coordinate system. Suppose that the effective pinhole is
located at the point ![]() . Then, again without loss of generality,
we can assume that the z-axis
. Then, again without loss of generality,
we can assume that the z-axis ![]() lies in the direction
lies in the direction
![]() . Moreover, since perspective projection
is rotationally symmetric about any line through
. Moreover, since perspective projection
is rotationally symmetric about any line through ![]() , the
mirror can be assumed to be a surface of revolution about the z-axis
, the
mirror can be assumed to be a surface of revolution about the z-axis
![]() . Therefore, we work in the 2-D cartesian frame
. Therefore, we work in the 2-D cartesian frame
![]() where
where ![]() is a unit vector orthogonal to
is a unit vector orthogonal to ![]() , and try to find the
2-dimensional profile of the mirror z(r) = z(x,y) where
, and try to find the
2-dimensional profile of the mirror z(r) = z(x,y) where
![]() . Finally, if the distance from
. Finally, if the distance from ![]() to
to
![]() is denoted by the parameter c, we have
is denoted by the parameter c, we have
![]() and
and ![]() . See
Figure 1 for an illustration
. See
Figure 1 for an illustration![[*]](foot_motif.gif) of the coordinate frame.
of the coordinate frame.
![]() . Suppose that this ray intersects
the mirror at the point (z,r). Then, since we assume that it also
passes through the origin
. Suppose that this ray intersects
the mirror at the point (z,r). Then, since we assume that it also
passes through the origin ![]() we have the relationship:
we have the relationship: